CF811E Vladik and Entertaining Flags

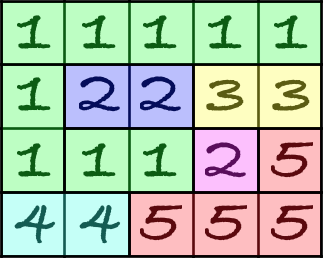
在空闲时间，Vladik 喜欢评估旗帜的美感。 每面旗帜可以表示为一个 $n×m$ 的矩阵，矩阵内的元素均为正整数。 我们将旗帜的美感定义为其矩阵中的连通块数。所谓连通块，是指一组拥有相同数字的格子，这些格子之间可以通过一条路径相连，路径上的任意两个格子都属于同一个连通块，即他们的数字相同且相邻。下面是一个将某面旗帜矩阵划分为连通块的示例：  但这一次，他决定稍作改变。现在他想评估的不是整个旗帜，而是某一段旗帜。旗帜的某一段可以用旗帜矩阵的一个子矩阵来描述，该子矩阵的对角顶点为 $(1,l)$ 和 $(n,r)$，其中 $1\leq l\leq r\leq m$。 请你帮助 Vladik 计算给定旗帜某些区间的美感值。

第一行包含三个用空格分隔的整数 $n$、$m$、$q$（$1\leq n\leq 10$，$1\leq m,q\leq 10^5$），分别表示旗帜矩阵的行数、列数和查询个数。 接下来的 $n$ 行，每行包含 $m$ 个用空格分隔的正整数，描述旗帜矩阵。矩阵中所有元素为不超过 $10^6$ 的正整数。 接下来的 $q$ 行，每行包含两个用空格分隔的整数 $l$ 和 $r$（$1\leq l\leq r\leq m$），代表一组区间，Vladik 需要你帮他计算该区间的美感。

对于每个查询，输出一行答案，表示对应区间的美感值。

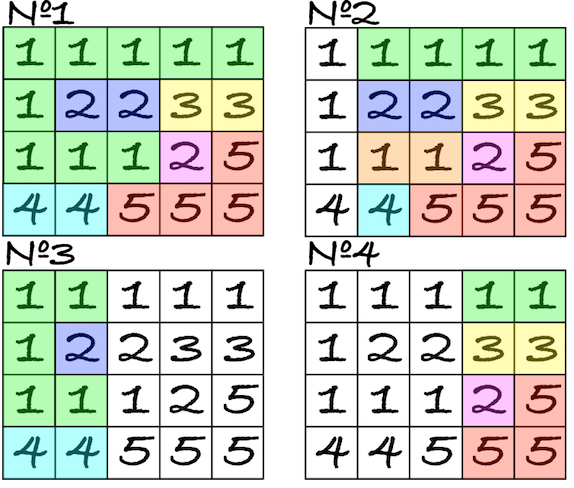
关于第一个测试用例中每个区间的连通块划分示例：  由 ChatGPT 5 翻译