CF814D An overnight dance in discotheque

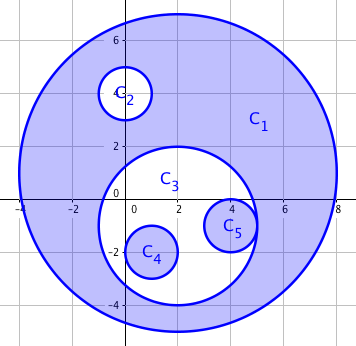
即使舞厅里人山人海，也不会阻止我们的朋友们尽情娱乐，不过如果能稍微宽敞一点，也不错，不是吗？ 可以把舞厅看作一个无限大的 $xy$ 平面，其中共有 $n$ 个舞者。每当某个人开始活动时，他/她只会在自己的活动范围内移动，这个活动范围是一个以 $(x_{i}, y_{i})$ 为圆心、$r_{i}$ 为半径的圆形区域 $C_{i}$。任意两个活动范围的边界至多有一个公共点，也就是说，对于每一对 $(i, j)$（$1 \leq i < j \leq n$），活动范围 $C_{i}$ 和 $C_{j}$ 要么没有交集，要么其中一个是另一个的子集。注意，可能会有两个人的活动范围的边界有且仅有一个公共点，但不会有两名舞者的活动范围完全相同。 月火（Tsukihi）把“宽敞度”定义为被奇数个正在移动的舞者的活动范围覆盖的面积。下图中，阴影部分表示如果所有人一起活动时的宽敞度。  然而，没有人会整个晚上都在移动，因此整晚被分为两半——午夜前和午夜后。每个舞者在其中一个时段活动，在另一个时段和朋友们坐下休息。两段时间的宽敞度分别计算，然后将其求和，当然，这个和应尽可能大。下图展示了上例中的一个最优方案。  通过不同的分配策略，决定谁在前半夜活动，谁在后半夜活动，可以得到不同的宽敞度和。你需要计算这个宽敞度和的最大可能值。

第一行包含一个正整数 $n$（$1 \leq n \leq 1000$）——表示舞者的数量。 接下来 $n$ 行，每行描述一名舞者：第 $i$ 行包含三个用空格分隔的整数 $x_{i}$、$y_{i}$ 和 $r_{i}$（$-10^{6} \leq x_{i}, y_{i} \leq 10^{6}$，$1 \leq r_{i} \leq 10^{6}$），表示以 $(x_{i}, y_{i})$ 为圆心、$r_{i}$ 为半径的圆形活动范围。

输出一个十进制小数，表示整个夜晚两段时间宽敞度的最大可能和。 如果你的结果的相对或绝对误差不超过 $10^{-9}$，则认为答案正确。形式化地说，设你的答案为 $a$，标准答案为 $b$，如果满足 $|a - b| \leq 10^{-9} \max(1, |b|)$ 则你的答案被认为是正确的。

第一个样例对应说明中的示意图。 由 ChatGPT 5 翻译