CF815A Karen and Game

On the way to school, Karen became fixated on the puzzle game on her phone! The game is played as follows. In each level, you have a grid with $ n $ rows and $ m $ columns. Each cell originally contains the number $ 0 $ . One move consists of choosing one row or column, and adding $ 1 $ to all of the cells in that row or column. To win the level, after all the moves, the number in the cell at the $ i $ -th row and $ j $ -th column should be equal to $ g_{i,j} $ . Karen is stuck on one level, and wants to know a way to beat this level using the minimum number of moves. Please, help her with this task!

The first line of input contains two integers, $ n $ and $ m $ ( $ 1

If there is an error and it is actually not possible to beat the level, output a single integer -1. Otherwise, on the first line, output a single integer $ k $ , the minimum number of moves necessary to beat the level. The next $ k $ lines should each contain one of the following, describing the moves in the order they must be done: - row $ x $ , ( $ 1

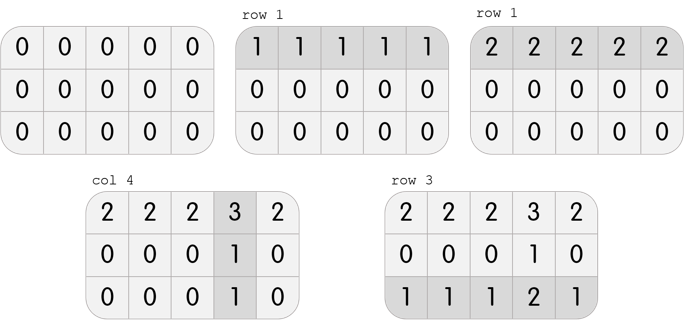In the first test case, Karen has a grid with $ 3 $ rows and $ 5 $ columns. She can perform the following $ 4 $ moves to beat the level: In the second test case, Karen has a grid with $ 3 $ rows and $ 3 $ columns. It is clear that it is impossible to beat the level; performing any move will create three $ 1 $ s on the grid, but it is required to only have one $ 1 $ in the center. In the third test case, Karen has a grid with $ 3 $ rows and $ 3 $ columns. 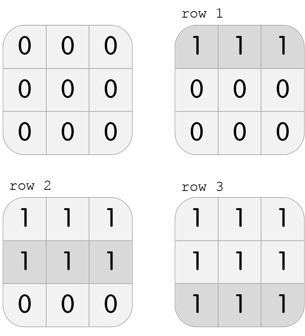She can perform the following $ 3 $ moves to beat the level: Note that this is not the only solution; another solution, among others, is col 1, col 2, col 3.