CF819B Mister B and PR Shifts

Some time ago Mister B detected a strange signal from the space, which he started to study. After some transformation the signal turned out to be a permutation $ p $ of length $ n $ or its cyclic shift. For the further investigation Mister B need some basis, that's why he decided to choose cyclic shift of this permutation which has the minimum possible deviation. Let's define the deviation of a permutation $ p $ as 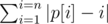. Find a cyclic shift of permutation $ p $ with minimum possible deviation. If there are multiple solutions, print any of them. Let's denote id $ k $ ( $ 0

First line contains single integer $ n $ ( $ 2

Print two integers: the minimum deviation of cyclic shifts of permutation $ p $ and the id of such shift. If there are multiple solutions, print any of them.

In the first sample test the given permutation $ p $ is the identity permutation, that's why its deviation equals to $ 0 $ , the shift id equals to $ 0 $ as well. In the second sample test the deviation of $ p $ equals to $ 4 $ , the deviation of the $ 1 $ -st cyclic shift $ (1,2,3) $ equals to $ 0 $ , the deviation of the $ 2 $ -nd cyclic shift $ (3,1,2) $ equals to $ 4 $ , the optimal is the $ 1 $ -st cyclic shift. In the third sample test the deviation of $ p $ equals to $ 4 $ , the deviation of the $ 1 $ -st cyclic shift $ (1,3,2) $ equals to $ 2 $ , the deviation of the $ 2 $ -nd cyclic shift $ (2,1,3) $ also equals to $ 2 $ , so the optimal are both $ 1 $ -st and $ 2 $ -nd cyclic shifts.