CF820B Mister B and Angle in Polygon

On one quiet day all of sudden Mister B decided to draw angle $ a $ on his field. Aliens have already visited his field and left many different geometric figures on it. One of the figures is regular convex $ n $ -gon (regular convex polygon with $ n $ sides). That's why Mister B decided to use this polygon. Now Mister B must find three distinct vertices $ v_{1} $ , $ v_{2} $ , $ v_{3} $ such that the angle  (where $ v_{2} $ is the vertex of the angle, and $ v_{1} $ and $ v_{3} $ lie on its sides) is as close as possible to $ a $ . In other words, the value 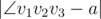 should be minimum possible. If there are many optimal solutions, Mister B should be satisfied with any of them.

First and only line contains two space-separated integers $ n $ and $ a $ ( $ 3

Print three space-separated integers: the vertices $ v_{1} $ , $ v_{2} $ , $ v_{3} $ , which form . If there are multiple optimal solutions, print any of them. The vertices are numbered from $ 1 $ to $ n $ in clockwise order.

In first sample test vertices of regular triangle can create only angle of $ 60 $ degrees, that's why every possible angle is correct. Vertices of square can create $ 45 $ or $ 90 $ degrees angles only. That's why in second sample test the angle of $ 45 $ degrees was chosen, since $ |45-67|<|90-67| $ . Other correct answers are: "3 1 2", "3 2 4", "4 2 3", "4 3 1", "1 3 4", "1 4 2", "2 4 1", "4 1 3", "3 1 4", "3 4 2", "2 4 3", "2 3 1", "1 3 2", "1 2 4", "4 2 1". In third sample test, on the contrary, the angle of $ 90 $ degrees was chosen, since $ |90-68|<|45-68| $ . Other correct answers are: "2 1 4", "3 2 1", "1 2 3", "4 3 2", "2 3 4", "1 4 3", "3 4 1".