CF821B Okabe and Banana Trees
题目描述
冈部由于某种奇怪的原因需要香蕉来进行实验。因此他决定去森林里砍香蕉树。
在二维平面上的点 $(x, y)$,其中 $x$ 和 $y$ 都是整数且 $0 \leq x, y$ ,每个这样的点上都有一棵树,这棵树上有 $x + y$ 个香蕉。其他点上没有树,也没有香蕉。现在,冈部画出了一条方程为 $y = -\frac{1}{m} x + b$ 的直线。冈部可以选择一个边平行于坐标轴的矩形,这个矩形的所有点都在该直线之下或在直线上,然后把这个矩形内边界上或内部的所有树砍下,把它们的香蕉全部带走。冈部选定的矩形可以退化,也就是说,可以是一个线段,甚至是一个点。
请帮助冈部明智地选择矩形,使得他可以获得最多的香蕉。
冈部确信答案不会超过 $10^{18}$。你可以相信他。
输入格式
输入的第一行包含两个用空格分隔的整数 $m$ 和 $b$,满足 $1 \leq m \leq 1000$,$1 \leq b \leq 10000$。
输出格式
输出冈部最多能够获得的香蕉总数。
说明/提示
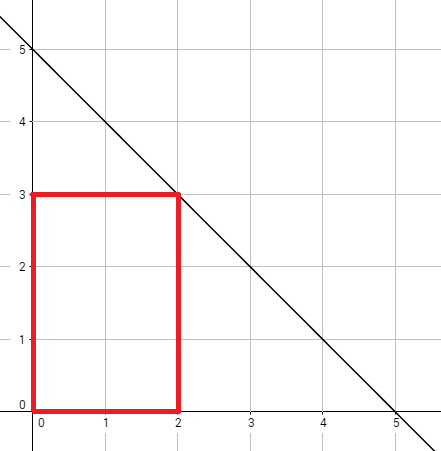
下图是样例 1 的对应图像。最优的矩形用红色标出,共有 $30$ 个香蕉。
由 ChatGPT 5 翻译