CF821E Okabe and El Psy Kongroo
题目描述
Okabe 喜欢散步,但他知道“机构”的间谍可能无处不在,这就是为什么他想知道在他的城市中有多少种不同且安全的散步方式。Okabe 的城市可以表示为所有满足 $x$ 和 $y$ 均为非负整数的点 $ (x, y) $。Okabe 从原点(点 $ (0, 0) $)出发,需要到达点 $ (k, 0) $。如果 Okabe 当前在点 $ (x, y) $,他每一步可以移动到 $ (x+1, y+1) $、$ (x+1, y) $ 或 $ (x+1, y-1) $。
此外,有 $n$ 条水平线段,第 $i$ 条线段从 $x=a_{i}$ 到 $x=b_{i}$(包括两端),高度为 $y=c_{i}$。保证 $a_{1}=0$,$a_{n} \leq k \leq b_{n}$,并且对于 $2 \leq i \leq n$,有 $a_{i}=b_{i-1}$。当 $x$ 满足 $a_{i} \leq x \leq b_{i}$ 时,第 $i$ 条线段要求 Okabe 的 $y$ 值必须在 $0 \leq y \leq c_{i}$ 的范围内,否则他可能会被间谍发现。这也意味着,当一条线段结束、另一条线段开始时,Okabe 需要同时满足两条线段的 $y$ 限制。
Okabe 现在想知道,从原点到达点 $(k, 0)$ 并且满足上述条件的所有路径数量是多少,答案对 $10^{9}+7$ 取模。
输入格式
输入的第一行包含两个整数 $n$ 和 $k$($1 \leq n \leq 100$,$1 \leq k \leq 10^{18}$)——线段的数量和目的地的 $x$ 坐标。
接下来的 $n$ 行,每行包含三个用空格分隔的整数 $a_{i}$、$b_{i}$ 和 $c_{i}$($0 \leq a_{i} < b_{i} \leq 10^{18}$,$0 \leq c_{i} \leq 15$)——第 $i$ 条线段的起点、终点及其 $y$ 坐标。
保证 $a_{1}=0$,$a_{n} \leq k \leq b_{n}$,且对于 $2 \leq i \leq n$,有 $a_{i} = b_{i-1}$。
输出格式
输出满足条件的从 $(0,0)$ 到 $(k,0)$ 的路径数量,结果对 $1000000007$($10^{9}+7$)取模。
说明/提示
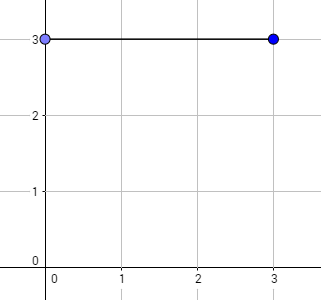 上图对应样例 1。所有合法路径为:
- 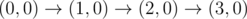
- 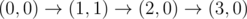
- 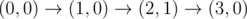
- 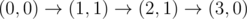
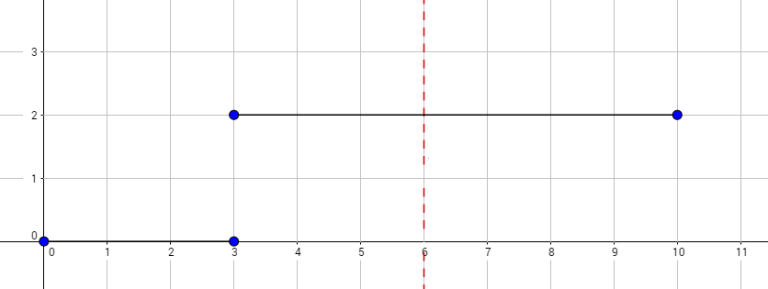 上图对应样例 2。Okabe 到达 $(3,0)$ 只有一条路径。之后所有合法路径为:
- 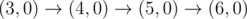
- 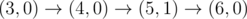
- 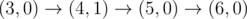
- 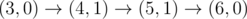
由 ChatGPT 5 翻译