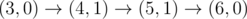CF821E Okabe and El Psy Kongroo

Okabe likes to take walks but knows that spies from the Organization could be anywhere; that's why he wants to know how many different walks he can take in his city safely. Okabe's city can be represented as all points $ (x,y) $ such that $ x $ and $ y $ are non-negative. Okabe starts at the origin (point $ (0,0) $ ), and needs to reach the point $ (k,0) $ . If Okabe is currently at the point $ (x,y) $ , in one step he can go to $ (x+1,y+1) $ , $ (x+1,y) $ , or $ (x+1,y-1) $ . Additionally, there are $ n $ horizontal line segments, the $ i $ -th of which goes from $ x=a_{i} $ to $ x=b_{i} $ inclusive, and is at $ y=c_{i} $ . It is guaranteed that $ a_{1}=0 $ , $ a_{n}

The first line of input contains the integers $ n $ and $ k $ ( $ 1

Print the number of walks satisfying the conditions, modulo $ 1000000007 $ ( $ 10^{9}+7 $ ).

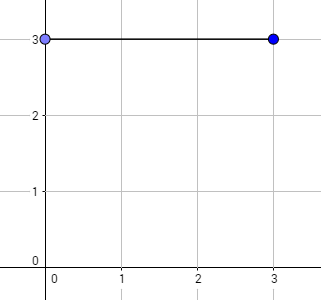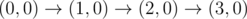
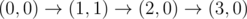
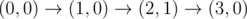
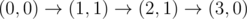
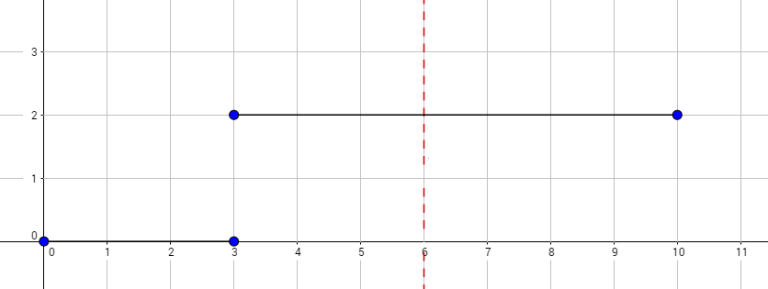The graph above corresponds to sample 1. The possible walks are: -  -  -  -  The graph above corresponds to sample 2. There is only one walk for Okabe to reach $ (3,0) $ . After this, the possible walks are: -  -  -  -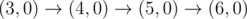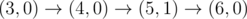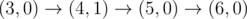