CF822F Madness
题目描述
帕夫洛波利斯大学的新学期开始了。假期结束后,Noora 需要从 Vičkopolis 返回帕夫洛波利斯继续她的学业。
有时候(或者说经常),总会有人不喜欢你。Noora 恰好有这样一位老师。他叫 Yury Dmitrievich,教授图论。Yury Dmitrievich 不喜欢 Noora,所以总是给她最难的任务。这一次依然如此。
老师给了 Noora 一棵有 $n$ 个结点的树。结点编号为 $1$ 到 $n$ 的整数。这棵树所有的边长度都是 $1$。Noora 需要选择一些简单路径,这些路径两两之间在边上没有交集。但每个结点必须属于至少一条被选中的路径。
对于每条被选中的路径,会进行如下操作:
1. 在这条路径上选择恰好一条边 $(u,v)$。
2. 在被选中的边 $(u,v)$ 上有一个点,距离结点 $u$ 的距离为 $x$,距离结点 $v$ 的距离为 $1-x$。Noora 可以任意选择 $x$,每条边的 $x$ 可以不同。
3. 选择 $u$ 或 $v$ 其中一个结点。点将开始朝被选结点的方向移动。
让我们通过一个例子说明点的移动过程。假设路径包含两条边 $(v_{1},v_{2})$ 和 $(v_{2},v_{3})$,点一开始在边 $(v_{1},v_{2})$ 上,并开始朝结点 $v_{1}$ 移动。那么点会到达 $v_{1}$,此时到达了路径的端点,于是“转身”向另一个方向移动,到达 $v_{2}$,然后移动到 $v_{3}$,再次“转身”,再回到 $v_{2}$,如此反复。点以 $1$ 条边每秒的速度移动。例如,$0.5$ 秒内,点会移动相当于半条边的长度。
每个结点上都装有一个秒表,一开始所有秒表的时间都是 $0$ 秒。所有点同时从各自选定的位置,按照各自的方向开始同时移动,秒表同时开始计时。当某个点到达结点 $v$ 时,$v$ 处的秒表会自动归零,也就是重新从零开始计时。
记 $res_{v}$ 表示如果点的移动持续无限长时间,结点 $v$ 处秒表所能显示的最大时间。Noora 需要选择路径和路径上的点的位置,使得 $res_{1}$ 尽可能小。如果有多个方案能够达到最小的 $res_{1}$,则需依次最小化 $res_{2}$、$res_{3}$、$res_{4},\ldots,res_{n}$。
请帮助 Noora 完成老师的任务。
为了帮助理解题意,请参考题目中示例的解释。
输入格式
第一行包含一个整数 $n$($2\leq n\leq 100$),表示树的结点数。
接下来 $n-1$ 行,每行包含两个整数 $u$ 和 $v$($1\leq u,v\leq n, u\neq v$),表示结点 $u$ 和结点 $v$ 之间有一条边。
保证输入数据构成一棵合法的树。
输出格式
第一行输出一个整数 $paths$,表示你选择的路径数。
接下来 $paths$ 行,每行描述一条路径,具体格式如下:
1. 一个整数 $len$,表示该路径包含的边数。
2. $len$ 个整数,表示路径上各条边的编号。边的编号按照输入顺序从 $1$ 到 $n-1$。
3. 两个整数 $u$ 和 $v$,表示你要在 $(u, v)$ 边上放置点,并且点将朝结点 $v$ 移动(注意输出顺序,若输出 "1 2" 则点朝 $2$ 移动,若输出 "2 1" 则点朝 $1$ 移动)。
4. 一个实数 $x$ ($0\leq x\leq 1$),表示点距离 $u$ 的距离($u$ 是上一项中的第一个数)。
记分方式:
评测系统会基于你的输出数据生成 $res$ 数组,同时会根据标准答案生成 $resOptimal$。仅当对每个 $i$($1\leq i\leq n$),有 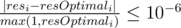 时,你的答案才会被接受。
说明/提示
考虑一个示例。
初始时刻,点的位置如下:
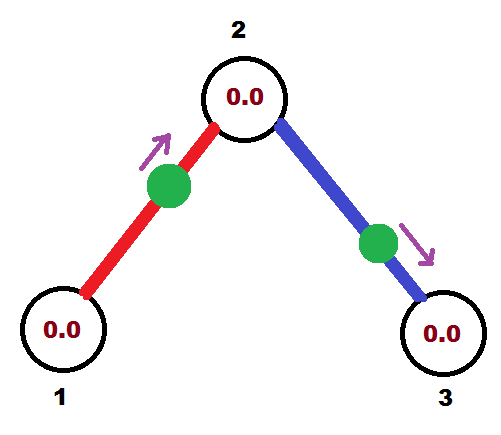
红色是第一条路径,蓝色是第二条路径,绿色圆圈为选择的点,棕色的数字表示当前秒表的数值,紫色箭头表示点的运动方向。
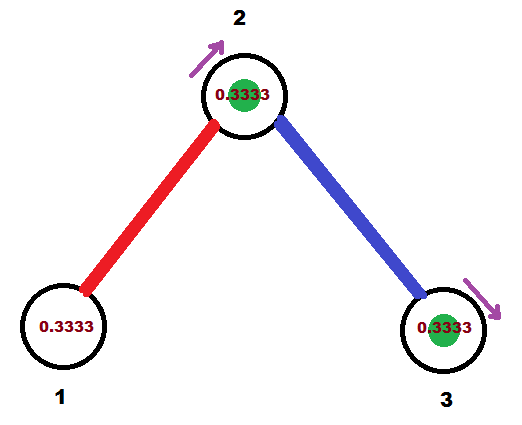
$0.(3)$ 秒后,所有点的位置如下(秒表还未归零):
归零后:
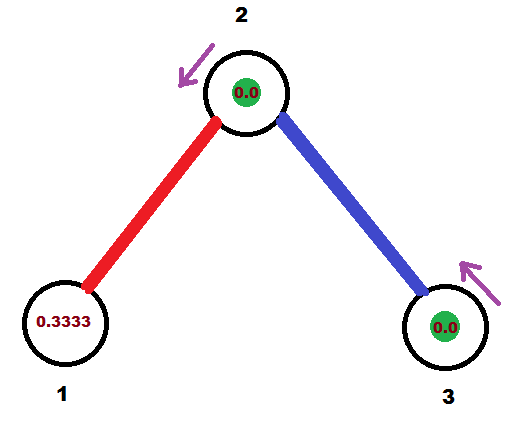
$1.0$ 秒后:
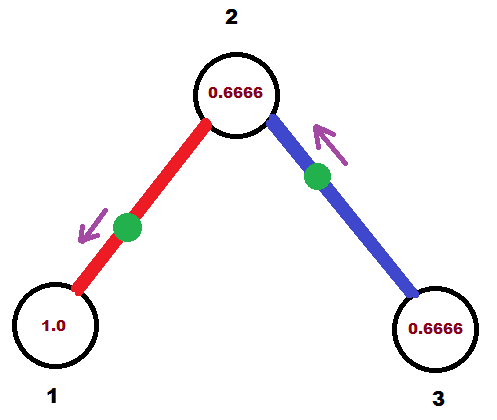
$1.(3)$ 秒后(又归零):
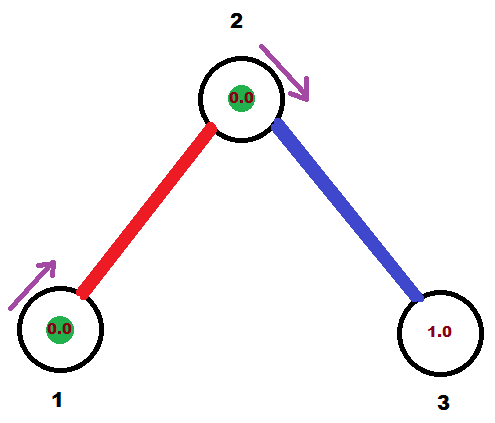
$2$ 秒后,所有点回到各自初始位置。
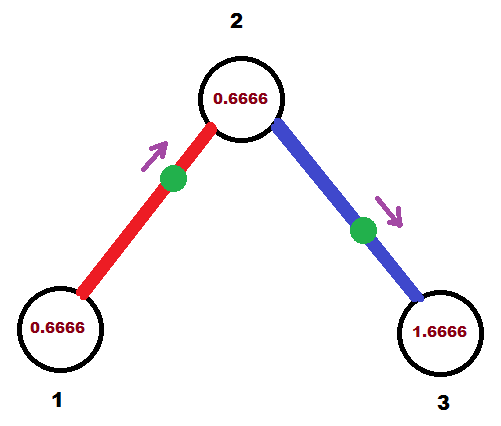
这个过程会无限重复下去。
由 ChatGPT 5 翻译