CF833E Caramel Clouds


众所周知，香草松饼是 Sweetland 花坛的最佳装饰。这种植物的幼苗需要阳光才能成长。Slastyona 有 $m$ 株幼苗，其中第 $j$ 株幼苗需要至少 $k_{j}$ 分钟的日照才能成熟。 Sweetland 大部分时间都是晴天，但有时会出现焦糖云。第 $i$ 朵云会在时间点（分钟）$l_{i}$ 出现，并在时间点 $r_{i}$ 消失。云朵会投下阴影，当至少有一朵云遮挡阳光时，幼苗无法生长。 Slastyona 希望她的松饼尽快成熟。她拥有恰好 $C$ 颗糖果，这是 Sweetland 的主要货币。 每朵云可以通过支付 $c_{i}$ 颗糖果来驱散。但根据 Sweetland 气象局的规定，任何人最多只能驱散两朵云。 Slastyona 尚未决定在公主的花园中种植哪株幼苗，因此她需要你的帮助。对于每株幼苗，请确定在遵守法律且不超支糖果的前提下，它能够成熟的最早时刻。注意每株幼苗的判定是独立的。 幼苗从时间点 $0$ 开始生长。

第一行包含两个整数 $n$ 和 $C$ $(0 \leq n \leq 3·10^{5}, 0 \leq C \leq 10^{9})$ —— 焦糖云的数量和 Slastyona 拥有的糖果数。 接下来 $n$ 行，每行包含三个整数 $l_{i}, r_{i}, c_{i}$ $(0 \leq l_{i}, r_{i} \leq 10^{9}, 0 \leq c_{i} \leq 10^{9})$，描述一朵焦糖云。 接下来一行包含一个整数 $m$ $(1 \leq m \leq 3·10^{5})$ —— 幼苗的数量。每株幼苗由一个整数 $k_{j}$ $(1 \leq k_{j} \leq 10^{9})$ 描述，表示所需的晴朗分钟数。

对于每株幼苗，输出一个整数 —— Slastyona 能让它成熟的最早分钟数。

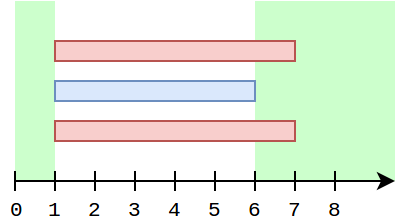
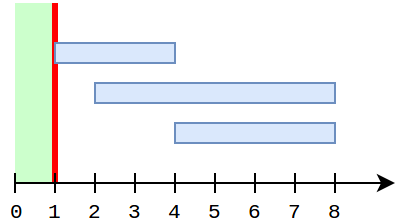
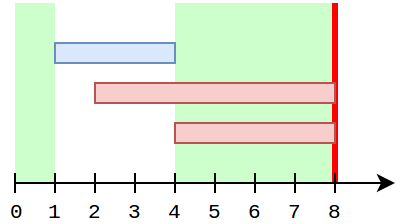
考虑第一个样例。对于每个 $k$，最优策略是驱散云朵 $1$ 和 $3$。剩余的云朵会在时间区间 $[1..6]$ 投下阴影。因此，区间 $[0..1]$ 和 $[6..\text{inf})$ 是晴朗的。  在第二个样例中，对于 $k=1$ 不需要驱散任何云朵；对于 $k=5$，最佳策略是驱散云朵 $2$ 和 $3$。这会新增晴朗区间 $[4..8]$，与 $[0..1]$ 结合后，使得幼苗能在第 $8$ 分钟成熟。  在第三个样例中，两株幼苗的情况完全不同。对于第一株，需要驱散云朵 $1$ 以获得晴朗区间 $[0..10]$。然而同样的策略对第二株幼苗的答案是 $180$。若改为驱散云朵 $2$，则形成晴朗区间 $[0..3]$ 和 $[7..\text{inf})$，可将时间缩短至 $104$ 分钟。  翻译由 DeepSeek R1 完成