CF838E Convex Countour
Description
You are given an strictly convex polygon with $ n $ vertices. It is guaranteed that no three points are collinear. You would like to take a maximum non intersecting path on the polygon vertices that visits each point at most once.
More specifically your path can be represented as some sequence of distinct polygon vertices. Your path is the straight line segments between adjacent vertices in order. These segments are not allowed to touch or intersect each other except at the vertices in your sequence.
Given the polygon, print the maximum length non-intersecting path that visits each point at most once.
Input Format
The first line of input will contain a single integer $ n $ ( $ 2
Output Format
Print a single floating point number, representing the longest non-intersecting path that visits the vertices at most once.
Your answer will be accepted if it has absolute or relative error at most $ 10^{-9} $ . More specifically, if your answer is $ a $ and the jury answer is $ b $ , your answer will be accepted if 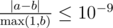.
Explanation/Hint
One optimal path is to visit points 0,1,3,2 in order.