CF843C Upgrading Tree

给你一棵有 $n$ 个顶点的树，你可以对其进行不超过 $2n$ 次变换。一次变换由三个顶点 $x,y,y'$ 定义，过程为删除边 $(x,y)$ 并添加边 $(x,y')$。当且仅当以下条件全部满足时，可以执行该变换： 1. 当前树中包含边 $(x,y)$。 2. 变换后，图仍然是一棵树。 3. 删除边 $(x,y)$ 后，树会被分成两个连通块。设包含顶点 $x$ 的块中节点的集合为 $V_x$，包含顶点 $y$ 的块中节点的集合为 $V_y$。必须满足 $|V_x|>|V_y|$，即包含 $x$ 的块的大小严格大于包含 $y$ 的块。 你需要通过不超过 $2n$ 次变换，使得到的树中所有点对之间距离的平方和最小，并输出一组实现这一目标的变换序列。 注意，你无需最小化操作次数，只需最小化所有点对之间距离的平方和。

第一行输入一个整数 $n$（$1 \leq n \leq 2 \times 10^5$），表示树的顶点数。 接下来的 $n-1$ 行，每行输入两个整数 $a$ 和 $b$（$1 \leq a, b \leq n, a \ne b$），表示一条树边。保证所给的边形成一棵树。

第一行输出整数 $k$（$0 \leq k \leq 2n$），表示构造中使用的变换次数。 接下来的 $k$ 行，每行三个整数 $x,y,y'$，表示一次变换。 当 $y = y'$ 时，允许输出变换（即使该变换不会改变树的结构），前提是变换的条件被满足。 如果有多组可行答案，输出任意一组即可。

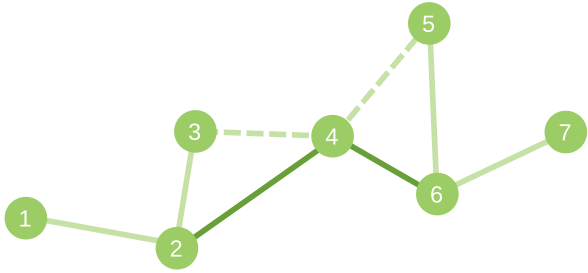
下图展示了第二个样例的情形。新增的边为加粗黑线，被删除的边为虚线。  由 ChatGPT 5 翻译