CF843D Dynamic Shortest Path
题目描述
给定一个带权有向图,包含 $n$ 个顶点和 $m$ 条边。你需要回答 $q$ 个两种类型的询问:
- $1\ v$ —— 查询从顶点 $1$ 到顶点 $v$ 的最短路径长度。
- $2\ c\ l_{1}\ l_{2}\ ...\ l_{c}$ —— 对编号为 $l_{1}, l_{2}, ..., l_{c}$ 的边的权值各加 $1$。
输入格式
输入数据的第一行包含三个整数 $n$、$m$、$q$($1 \leq n, m \leq 10^{5}$,$1 \leq q \leq 2000$),分别表示图中的顶点数、边数和询问数。
接下来的 $m$ 行描述边的信息:第 $i$ 行包含三个整数 $a_{i}$、$b_{i}$、$c_{i}$($1 \leq a_{i}, b_{i} \leq n$,$0 \leq c_{i} \leq 10^{9}$),表示编号为 $i$ 的边从顶点 $a_{i}$ 指向 $b_{i}$,初始权值为 $c_{i}$。
接下来的 $q$ 行,每行为一条询问,格式如上($1 \leq v \leq n$,$1 \leq l_{j} \leq m$)。保证每条第二类询问中的 $l_{j}$ 互不相同。且所有第二类操作涉及的边总数不超过 $10^6$。
输出格式
对于每一条第一类询问,输出一行,表示从顶点 $1$ 到顶点 $v$ 的最短路径长度。如果不存在这样的路径,输出 $-1$。
说明/提示
第一个样例中的图变动如下所示:
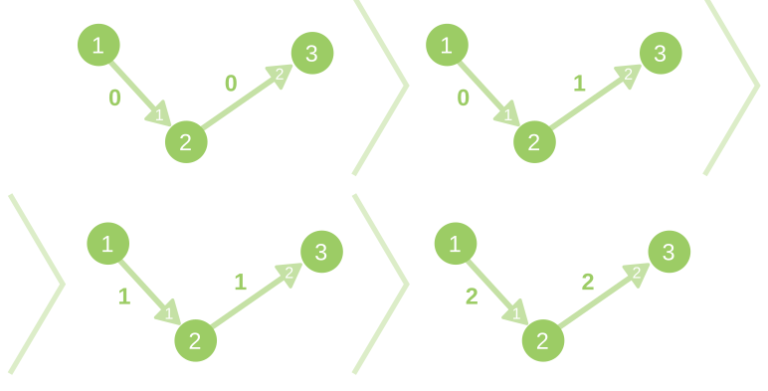
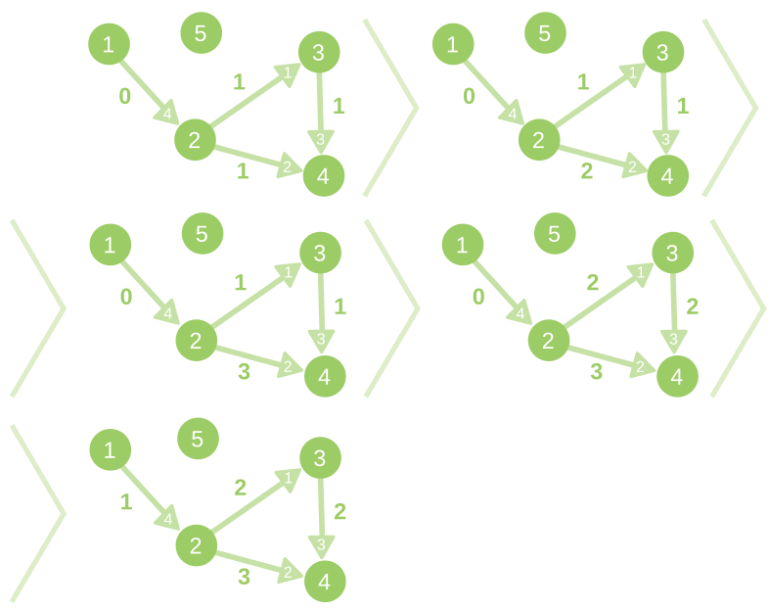
第二个样例中的图变动如下:
由 ChatGPT 5 翻译