CF843E Maximum Flow

给定一个包含 $n$ 个顶点和 $m$ 条边的有向图，顶点 $s$ 和 $t$ 分别被标记为源点和汇点。此外，没有边以 $s$ 为终点，也没有边以 $t$ 为起点。 该图的构造方式如下：最初，每条边都有容量 $c_{i}>0$。在此流网络中，以 $s$ 为源点、$t$ 为汇点，构造了一个最大流。我们用 $f_{i}$ 表示编号为 $i$ 的边上通过的流量。然后，所有容量 $c_{i}$ 和流量 $f_{i}$ 被擦除，取而代之的是每条边上标记了一个指标 $g_{i}$——如果编号为 $i$ 的边上流量为正（即 $f_{i}>0$），则 $g_{i}=1$，否则 $g_{i}=0$。 给定图和每条边的 $g_{i}$，请你求出初始流网络中可能被完全充满（即 $f_{i}=c_{i}$）的最少边数。同时，构造出使最大流成立的相应流网络。 在有向图中，流是指每条边上有流量 $f_{i}$，满足以下条件： - 对于每个顶点（除源点和汇点外），流入总量等于流出总量； - 对于每条边，有 $0 \le f_{i} \le c_{i}$。 最大流是指，从源点出发流出的流量总和（本题中没有流入源点的边），达到可能的最大值。

输入的第一行包含四个正整数 $n,m,s,t$（$2 \le n \le 100$，$1 \le m \le 1000$，$1 \le s,t \le n$，$s \ne t$），分别表示顶点数、边数、源点编号和汇点编号。 接下来的 $m$ 行，每行包含三个非负整数 $u_{i}$、$v_{i}$、$g_{i}$（$1 \le u_{i}, v_{i} \le n$，$u_{i} \ne v_{i}$），表示第 $i$ 条边的起点、终点和指标。若编号为 $i$ 的边上通过的流量为正，则 $g_{i}=1$；否则 $g_{i}=0$。 保证没有自环，并且每一对有序顶点间最多有一条边，并且至少存在一种满足输入约束的网络流。

输出第一行一个非负整数 $k$，表示在最大流中需要被完全充满（$f_{i}=c_{i}$）的最少边数。 接下来 $m$ 行，每行两个整数 $f_{i},c_{i}$（$1 \le c_{i} \le 10^{9}$，$0 \le f_{i} \le c_{i}$），表示第 $i$ 条边上的流量和容量。 所输出的数据必须构成一个正确的最大流网络，并恰好有 $k$ 条边满足 $f_{i}=c_{i}$。并且仅当 $g_{i}=1$ 时，$f_{i}>0$ 成立。 如果有多组答案，输出任意一组均可。

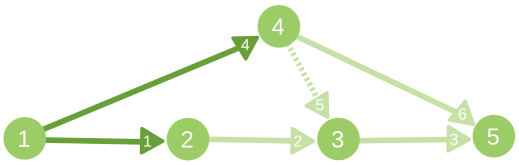
以下是第二组样例的示意图。被涂黑的边为已充满的边，$g_{i}=0$ 的边用虚线表示。边上的数字为输入中该边的编号。  由 ChatGPT 5 翻译