CF843E Maximum Flow

You are given a directed graph, consisting of $ n $ vertices and $ m $ edges. The vertices $ s $ and $ t $ are marked as source and sink correspondingly. Additionally, there are no edges ending at $ s $ and there are no edges beginning in $ t $ . The graph was constructed in a following way: initially each edge had capacity $ c_{i}>0 $ . A maximum flow with source at $ s $ and sink at $ t $ was constructed in this flow network. Let's denote $ f_{i} $ as the value of flow passing through edge with index $ i $ . Next, all capacities $ c_{i} $ and flow value $ f_{i} $ were erased. Instead, indicators $ g_{i} $ were written on edges — if flow value passing through edge $ i $ was positive, i.e. $ 1 $ if $ f_{i}>0 $ and $ 0 $ otherwise. Using the graph and values $ g_{i} $ , find out what is the minimum possible number of edges in the initial flow network that could be saturated (the passing flow is equal to capacity, i.e. $ f_{i}=c_{i} $ ). Also construct the corresponding flow network with maximum flow in it. A flow in directed graph is described by flow values $ f_{i} $ on each of the edges so that the following conditions are satisfied: - for each vertex, except source and sink, total incoming flow and total outcoming flow are equal, - for each edge $ 0

The first line of input data contains four positive integers $ n,m,s,t $ ( $ 2

In the first line print single non-negative integer $ k $ — minimum number of edges, which should be saturated in maximum flow. In each of next $ m $ lines print two integers $ f_{i},c_{i} $ ( $ 1

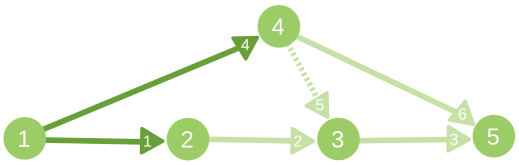
The illustration for second sample case. The saturated edges are marked dark, while edges with $ g_{i}=0 $ are marked with dotted line. The integer on edge is the index of this edge in input list.