CF847L Berland SU Computer Network

在 Berland 州立大学的计算机网络中，有 $n$ 个路由器，编号从 $1$ 到 $n$。有些路由器通过网线（patch cord）两两相连。信息可以在网线上双向传输。该网络结构保证任意两个路由器之间（直接或间接）都可以通信。网络没有环，因此每对路由器之间通过网线的路径唯一。 不幸的是，管理员丢失了网络的具体拓扑结构。为了恢复拓扑结构，收集到了以下辅助信息。 对于每条直接连接到路由器 $i$ 的网线 $p$，都知道相对于 $i$ 而言位于网线 $p$ 后方的路由器列表。换言之，所有从这些路由器到路由器 $i$ 的路径都经过 $p$。因此，对于每个路由器 $i$，有 $k_i$ 个列表，其中 $k_i$ 是连接到 $i$ 的网线数量。 例如，若网络由 $1$、$2$、$3$ 三个路由器组成，并按链式结构 $1-2-3$ 连接： - 路由器 $1$：唯一一条网线，其后方列表包含 $2$ 和 $3$。 - 路由器 $2$：每条网线都有一个列表，一个列表包含 $1$，另一个包含 $3$。 - 路由器 $3$：唯一一条网线，其后方列表包含 $1$ 和 $2$。 你的任务是帮助管理员恢复网络拓扑，即确定所有通过网线直接相连的路由器对。

第一行包含一个整数 $n$（$2 \leq n \leq 1000$），表示网络中的路由器数量。 接下来的 $n$ 行中，第 $i$ 行描述了路由器 $i$ 的所有列表。 每个列表先给出路由器数量，然后是一个冒号 ':'，随后是该列表中路由器的编号，编号间用逗号分隔。各个列表之间用符号 '-' 分隔。 保证对于每个路由器 $i$，所有列表中路由器的总数为 $n-1$，且列表中的所有编号互不相同。每个列表中不包含编号 $i$ 的路由器。

如果不存在满足条件的网络结构，输出 $-1$。 否则，第一行输出 $n-1$，即网线总数。之后的 $n-1$ 行中，每行输出一对通过网线直接相连的路由器编号。每条网线仅输出一次，顺序不限。

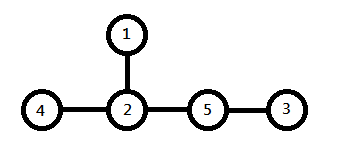
第一个样例已在题目描述中分析。 第二个样例的答案如下图所示。  第一个路由器有一个列表，包含了所有其它路由器。第二个路由器有三个列表：第一个只包含路由器 $4$，第二个只包含路由器 $1$，第三个包含路由器 $3$ 和 $5$。第三个路由器有一个列表，包含所有其它路由器。第四个路由器同样有一个列表，包含了所有其它路由器。第五个路由器有两个列表：第一个只包含路由器 $3$，第二个包含路由器 $1$、$2$ 和 $4$。 由 ChatGPT 5 翻译