CF848A From Y to Y

从开始到结束，这条消息一直在等待被传达。 给定一个含有 $n$ 个小写英文字母的无序多重集（“多重”表示同一个字母可以出现多次），我们将所有字母都视作长度为 $1$ 的字符串，并重复以下操作共 $n-1$ 次： - 从集合中任意取出两个元素 $s$ 和 $t$，并将它们连接后的结果 $s+t$ 加入集合。 该操作的代价定义为 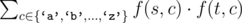，其中 $f(s,c)$ 表示字符 $c$ 在字符串 $s$ 中出现的次数。 给定一个非负整数 $k$，请构造任意一个满足条件的、至多包含 $100000$ 个字母的非空多重集，使得整个过程中最小累计代价恰好为 $k$。可以证明解一定存在。

输入的唯一一行包含一个非负整数 $k$（$0 \leq k \leq 100000$），表示所需的最小代价。

输出一个非空字符串，长度不超过 $100000$，该字符串表示满足要求的多重集中所有字母的拼接。 注意，输出的字符串不需要是合并操作后形成的最终字符串，仅需表示一个无序的字母多重集。

对于多重集 {'a', 'b', 'a', 'b', 'a', 'b', 'a', 'b'}，一种完成全部操作的方法如下： - {"ab", "a", "b", "a", "b", "a", "b"}，代价为 $0$； - {"aba", "b", "a", "b", "a", "b"}，代价为 $1$； - {"abab", "a", "b", "a", "b"}，代价为 $1$； - {"abab", "ab", "a", "b"}，代价为 $0$； - {"abab", "aba", "b"}，代价为 $1$； - {"abab", "abab"}，代价为 $1$； - {"abababab"}，代价为 $8$。 总代价为 $12$，并且这一定是该过程的最小总代价。 由 ChatGPT 5 翻译