CF848A From Y to Y

From beginning till end, this message has been waiting to be conveyed. For a given unordered multiset of $ n $ lowercase English letters ("multi" means that a letter may appear more than once), we treat all letters as strings of length $ 1 $ , and repeat the following operation $ n-1 $ times: - Remove any two elements $ s $ and $ t $ from the set, and add their concatenation $ s+t $ to the set. The cost of such operation is defined to be 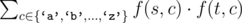, where $ f(s,c) $ denotes the number of times character $ c $ appears in string $ s $ . Given a non-negative integer $ k $ , construct any valid non-empty set of no more than $ 100000 $ letters, such that the minimum accumulative cost of the whole process is exactly $ k $ . It can be shown that a solution always exists.

The first and only line of input contains a non-negative integer $ k $ ( $ 0

Output a non-empty string of no more than $ 100000 $ lowercase English letters — any multiset satisfying the requirements, concatenated to be a string. Note that the printed string doesn't need to be the final concatenated string. It only needs to represent an unordered multiset of letters.

For the multiset {'a', 'b', 'a', 'b', 'a', 'b', 'a', 'b'}, one of the ways to complete the process is as follows: - {"ab", "a", "b", "a", "b", "a", "b"}, with a cost of $ 0 $ ; - {"aba", "b", "a", "b", "a", "b"}, with a cost of $ 1 $ ; - {"abab", "a", "b", "a", "b"}, with a cost of $ 1 $ ; - {"abab", "ab", "a", "b"}, with a cost of $ 0 $ ; - {"abab", "aba", "b"}, with a cost of $ 1 $ ; - {"abab", "abab"}, with a cost of $ 1 $ ; - {"abababab"}, with a cost of $ 8 $ . The total cost is $ 12 $ , and it can be proved to be the minimum cost of the process.