CF848B Rooter's Song

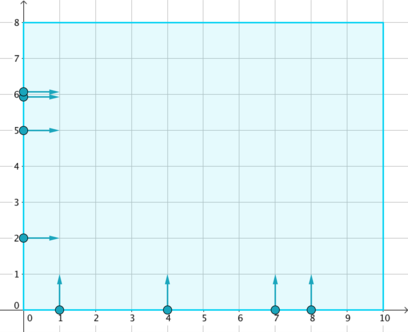
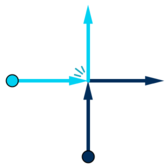
无论目的地在哪里，无论我们遇见谁，让我们一起演绎这首歌。 在一个笛卡尔坐标平面上，有一个大小为 $w \times h$ 的矩形舞台，表示为四个角分别为 $(0,0)$、$(w,0)$、$(w,h)$ 和 $(0,h)$ 的矩形。可以认为，在进入舞台之前不会发生碰撞。 舞台的边上站着 $n$ 位舞者。第 $i$ 位舞者属于以下两组之一： - 纵向舞者：站在 $(x_{i},0)$，沿正 $y$ 方向（向上）运动； - 横向舞者：站在 $(0,y_{i})$，沿正 $x$ 方向（向右）运动。  根据编舞，第 $i$ 位舞者在刚开始的 $t_{i}$ 毫秒内保持静止，然后以每毫秒 $1$ 个单位的速度按指定方向移动，直到到达另一个边界为止。保证没有两位舞者在同一组、同一位置且拥有相同的等待时间。 当两名舞者发生碰撞（即在二者都在移动时恰好处于同一点），他们会立刻交换移动方向并继续运动。  舞者在到达舞台边界时停止。请计算每位舞者最终的位置。

输入的第一行包含三个用空格分隔的正整数 $n$、$w$ 和 $h$（$1 \leq n \leq 100000$，$2 \leq w,h \leq 100000$）——舞者数量以及舞台的宽和高。 接下来 $n$ 行，每行描述一位舞者：第 $i$ 行包含三个用空格分隔的整数 $g_{i}$、$p_{i}$ 和 $t_{i}$（$1 \leq g_{i} \leq 2$，$1 \leq p_{i} \leq 99999$，$0 \leq t_{i} \leq 100000$），表示第 $i$ 位舞者的类型 $g_{i}$（$g_{i}=1$：纵向，$g_{i}=2$：横向）、位置和等待时间。如果 $g_{i}=1$，那么 $p_{i}=x_{i}$；否则 $p_{i}=y_{i}$。保证 $1 \leq x_{i} \leq w-1$ 且 $1 \leq y_{i} \leq h-1$。保证没有两位舞者在同一组、同一位置且拥有相同的等待时间。

输出 $n$ 行，其中第 $i$ 行包含两个用空格分隔的整数 $(x_{i},y_{i})$，表示输入中第 $i$ 位舞者的最终停止位置。

第一个样例对应题面图片的初始状态，各位舞者的运动轨迹在下图中用不同颜色标记。  在第二个样例中，舞者之间没有碰撞。 由 ChatGPT 5 翻译