CF848D Shake It!

一个永无止境、变化迅速而如梦似幻的世界展开了，当那扇神秘的大门开启。 一个“世界”是一个无序图 $G$ ，其顶点集合 $V(G)$ 中包含两个特殊顶点 $s(G)$ 和 $t(G)$。初始世界的顶点集合为 $\{s(G), t(G)\}$，两者之间有一条边连接。 在初始世界中共进行了 $n$ 次变化。每次变化时，向 $V(G)$ 中加入一个新顶点 $w$，选择一个已有的边 $(u, v)$，并分别添加两条新边 $(u, w)$ 和 $(v, w)$ 到 $E(G)$ 中。注意，同一条边可能在多次变化中被选择。 已知最终生成的图中，从 $s$ 到 $t$ 的最小割的容量为 $m$，即至少需要移除 $m$ 条边才能使 $s(G)$ 和 $t(G)$ 断开。 请计算在上述约束下，可以构造出多少个两两不相似的世界，结果对 $10^9+7$ 取模。我们定义两个世界是相似的，如果它们是同构的，并且同构映射中 $s$ 和 $t$ 的编号未被交换。也就是说，若存在 $V(G)$ 到 $V(H)$ 的双射 $f$，满足： - $f(s(G))=s(H)$； - $f(t(G))=t(H)$； - $u$ 和 $v$ 在 $G$ 中有边当且仅当 $f(u)$ 和 $f(v)$ 在 $H$ 中有边。

输入的第一行包含两个用空格分隔的整数 $n$ 和 $m$，表示共进行了 $n$ 次操作，最小割容量为 $m$。其中 $1\leq n, m \leq 50$。

输出一个整数，表示可以构造的不相似世界的数量，对 $10^9+7$ 取模。

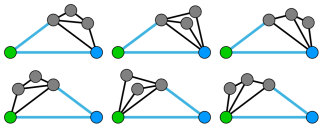
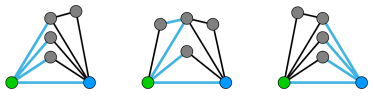
在第一个样例中，存在如下 $6$ 个两两不相似且满足约束的世界，其中 $s(G)$ 用绿色标记，$t(G)$ 用蓝色标记，某个最小割用浅蓝色表示。  在第二个样例中，存在如下 $3$ 个满足约束的世界。  由 ChatGPT 5 翻译