CF848E Days of Floral Colours

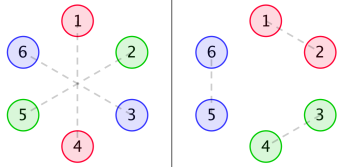
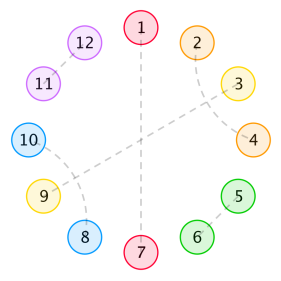
花卉时钟一直矗立在镜湖边。尽管不能留住时间，但它提醒人们时间的过去，使人们想起过去美好的时光。 在花卉时钟的边缘一共有 $2n$ 朵花，顺时针依次编号为 $1$ 到 $2n$，每一朵花的颜色为 $n$ 种可能的颜色中的一种。对于每种颜色，恰有两朵花是这种颜色的，这两朵花的距离要么不大于 $2$，要么等于 $n$。另外，如果花 $u$ 和花 $v$ 有相同的颜色，那么 $u$ 对面的那一朵花和 $v$ 对面的那一朵花的颜色也应该相同——对称是美的！ 形式化的说，两朵花之间的距离是 $1$ 加上夹在以这两朵花为端点的劣弧（或者半圆）之间的花的数目。下面是当 $n=6$ 时一种可能的安排颜色的方式：  我们定义一种安排方式的美感为被所有相对（距离为 $n$）且颜色相同的花分开的连续段的长度的乘积。换句话说，为了计算美感，我们先在环上移除那些与相对的花颜色相同的花。然后，它的美感就是剩下的连续段长度的乘积。注意到本题中包括了长度为 $0$ 的那些连续段。在某种安排方式中，如果没有任何一朵花使得与它相对的花的颜色与它相同，那么这种安排方式的美感为 $0$。比如说，上图的安排方式的美感等于 $1\times 3\times 1\times 3=9$———这些连续段为 $\{2\},\{4,5,6\},\{8\},\{10,11,12\}$。 尽管保持了这些约束条件，但是可能的安排方式会有多种，你需要计算出所有可能的安排方式的美感之和，对 $998244353$ 取模。两个安排方式被视为不同的，当且仅当存在一个二元组 $(u,v)(1\leq u,v\leq 2n)$ 使得在其中一种安排方式中花 $u$ 和花 $v$ 颜色相同而在另一种安排方式中颜色不同。 Translated By Karry5307

The first and only line of input contains a lonely positive integer $ n $ ( $ 3

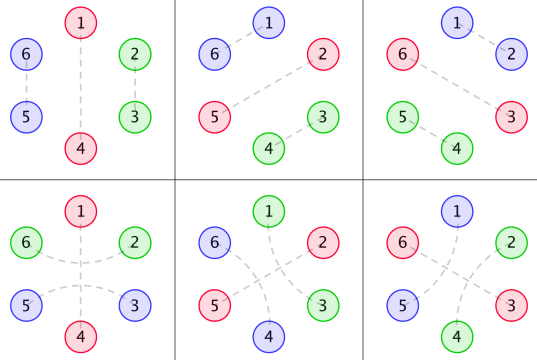
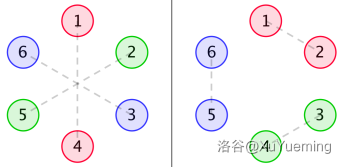
一行一个整数，代表所有可能的安排方式的美感之和，对 $998244353$ 取模。 ### 样例解释 当 $n=3$ 的时候，以下六种安排方式都有 $2\times 2=4$ 的美感  但是别的，比如说下图中左边那一种，美感为 $0$。右边的那一种不合法，因为它不对称。 

With $ n=3 $ , the following six arrangements each have a beauty of $ 2×2=4 $ . While many others, such as the left one in the figure below, have a beauty of $ 0 $ . The right one is invalid, since it's asymmetric.