CF850A Five Dimensional Points

给定 $n$ 个 $5$ 维空间中的点，这些点的编号从 $1$ 到 $n$，且任意两个点都不重合。 如果存在与点 $a$ 不同的点 $b$ 和 $c$，使得向量 $\overrightarrow{ab}$ 和 $\overrightarrow{ac}$ 之间的夹角为锐角（即严格小于 $90^\circ$），则称点 $a$ 为“坏的”。否则，点 $a$ 为“好的”。 在 $5$ 维空间中，向量 $\overrightarrow{u}$ 和 $\overrightarrow{v}$ 之间的夹角定义为 $\arccos\dfrac{\overrightarrow{u} \cdot \overrightarrow{v}}{|\overrightarrow{u}| \cdot |\overrightarrow{v}|}$，其中 $\overrightarrow{u} \cdot \overrightarrow{v}$ 为标量积，$|\overrightarrow{u}|$ 为向量 $\overrightarrow{u}$ 的长度。 给出这些点的坐标，输出所有“好”的点的编号，按升序排列。

第一行为一个整数 $n$（$1 \leq n \leq 10^{3}$），表示点的个数。 接下来的 $n$ 行，每行为 $a_i, b_i, c_i, d_i, e_i$（$|a_i|, |b_i|, |c_i|, |d_i|, |e_i| \leq 10^{3}$），表示第 $i$ 个点的五个坐标。所有点都不同。

首先输出一个整数 $k$，表示“好”的点的数量。 接下来输出 $k$ 个整数，各占一行，分别表示“好”的点的编号，按升序排列。

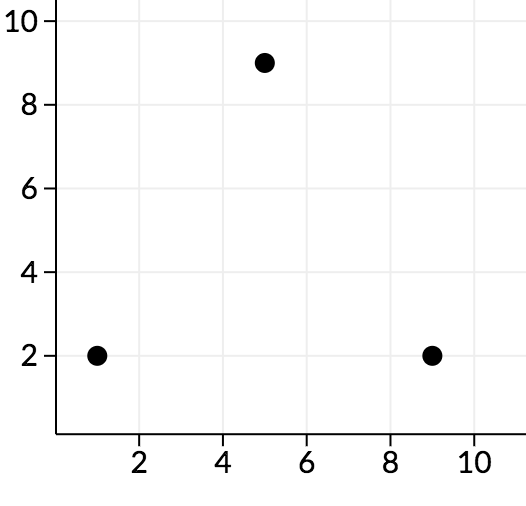
在第一个样例中，第一个点与所有其他点的任意一对构成的夹角恰好是 $90^\circ$，所以它是“好”的。 在第二个样例中，在 $cd$ 平面上，点的分布如下图所示：  可以看到这里所有夹角都是锐角，因此没有“好”的点。 由 ChatGPT 5 翻译