CF852C Property

Bill 是 BubbleLand 的著名数学家。凭借其革命性的数学发现，他赚了很多钱，建造了一座美丽的房子。不幸的是，因为没有按时缴纳房产税，法院决定惩罚 Bill，让他失去部分房产。 Bill 的房产可以看作是一个凸的正 $2n$ 边形 $A_{0}\ A_{1}...\ A_{2n-1}\ A_{2n}$，其中 $A_{2n}=A_{0}$，每条边的长度均为 $1$ 米。 法院剥夺房产的规则如下： - 将每条边 $A_{k}A_{k+1}$（$k=0,...,2n-1$）分成 $n$ 等份，每份长 $1/n$，分点为 $P_{0},\,P_{1},\,\ldots,\,P_{n-1}$。 - 在每条边 $A_{2k}A_{2k+1}$（$k=0,...,n-1$）上，法院会选择某个点 $B_{2k}=P_{i}$，其中 $i=0,...,n-1$，如图所示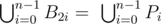： - 在每条边 $A_{2k+1}A_{2k+2}$（$k=0,...,n-1$）上，Bill 可以选择一个点 $B_{2k+1}=P_{i}$，其中 $i=0,...,n-1$，如图所示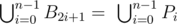： - Bill 将保留由 $2n$ 边形 $B_{0}\ B_{1}...\ B_{2n-1}$ 所围成的区域内的房产。 幸运的是，Bill 已经知道了法院选择的 $B_{2k}$ 的位置。尽管他是大数学家，但他的房子很大，计算起来很困难。因此，他请你帮忙选择最优的点，使得他能最大化所保留房产的面积。

第一行包含一个整数 $n$（$2\leq n\leq 50000$），表示 $2n$ 边形的边数的一半。 第二行包含 $n$ 个互不相同的整数 $B_{2k}$（$0\leq B_{2k}\leq n-1,\ k=0,...,n-1$），用空格隔开，表示法院在每条边 $A_{2k}A_{2k+1}$ 上选择的点。如果 $B_{2k}=i$，则表示法院在该边上选择了点 $P_{i}$。

输出 $n$ 个互不相同的整数，用空格隔开，分别表示 Bill 应该选择的点 $B_{1}, B_{3}, ..., B_{2n-1}$ 以最大化他能保留的房产面积。如果有多种选法都能达到最大面积，输出其中任意一种即可。

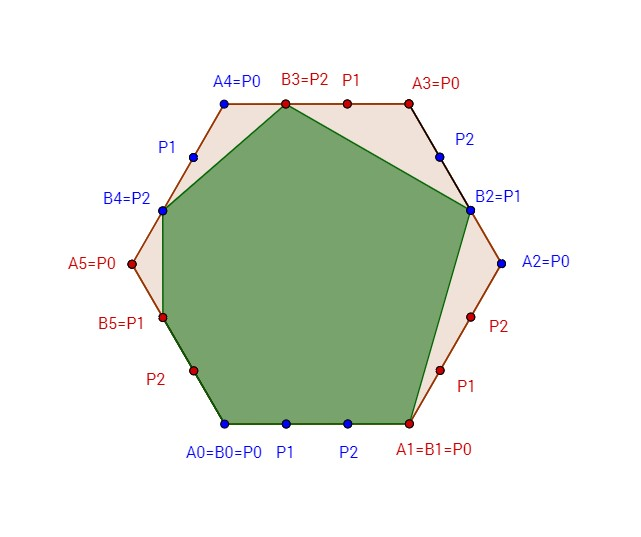
要想最大化面积，Bill 应该选择的点为：$B_{1}=P_{0}$，$B_{3}=P_{2}$，$B_{5}=P_{1}$。  由 ChatGPT 5 翻译