CF852F Product transformation

Consider an array $ A $ with $ N $ elements, all being the same integer $ a $ . Define the product transformation as a simultaneous update $ A_{i}=A_{i}·A_{i+1} $ , that is multiplying each element to the element right to it for 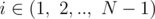, with the last number $ A_{N} $ remaining the same. For example, if we start with an array $ A $ with $ a=2 $ and $ N=4 $ , then after one product transformation $ A=[4,\ 4,\ 4,\ 2] $ , and after two product transformations $ A=[16,\ 16,\ 8,\ 2] $ . Your simple task is to calculate the array $ A $ after $ M $ product transformations. Since the numbers can get quite big you should output them modulo $ Q $ .

The first and only line of input contains four integers $ N $ , $ M $ , $ a $ , $ Q $ ( $ 7

You should output the array $ A $ from left to right.

The multiplicative order of a number $ a $ modulo $ Q $ 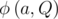, is the smallest natural number $ x $ such that $ a^{x}\ mod\ Q=1 $ . For example, 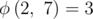.