CF853E Lada Malina
题目描述
经过长期研究和大量实验,Megapolia 汽车制造商「AutoVoz」推出了一款全新车型,名为「Lada Malina」。该车型最引人注目的特性之一是其高效且环保的发动机。
现在将一辆车视为 $Oxy$ 平面上的一个点。汽车配备有 $k$ 台编号为 $1$ 到 $k$ 的发动机。每台发动机通过其速度向量 $(vx_{i}, vy_{i})$(以距离单位/天计算)来定义。每台发动机可以以任意水平 $w_{i}$ 启动,其中 $w_{i}$ 是一个位于 $[-1, 1]$ 的实数,最终汽车的速度会加上 $(w_{i} \cdot vx_{i}, w_{i} \cdot vy_{i})$。也就是说,汽车最终的速度为:
$$(w_{1} \cdot vx_{1} + w_{2} \cdot vx_{2} + \cdots + w_{k} \cdot vx_{k},\ w_{1} \cdot vy_{1} + w_{2} \cdot vy_{2} + \cdots + w_{k} \cdot vy_{k})$$
具体来说,如果汽车在一天内始终保持各 $w_{i}$ 不变,$x$ 坐标将变化为上述表达式的第一项,$y$ 坐标将变化为第二项。例如,如果所有 $w_{i}$ 都为零,汽车不会移动;如只有 $w_{1}=1$,其余全为零,则汽车按第一个发动机的速度行驶。
Megapolia 有 $n$ 个工厂,第 $i$ 个工厂位于 $(fx_{i}, fy_{i})$,该工厂有 $a_{i}$ 辆已准备好的「Lada Malina」。
为提升新车销量,「AutoVoz」计划举办一场国际汽车展览。共有 $q$ 个展览举办地与时间的选项,第 $i$ 个选项的展览将在点 $(px_{i}, py_{i})$ 于 $t_{i}$ 天后举办。
当然,「AutoVoz」希望能把尽可能多的新车从工厂转运到展览地点。汽车会通过适当调整发动机启动水平,使得它们正好在展览开始时到达展览地点。
但对于某些选项,某些工厂的汽车可能无法按时赶到。你的任务是,针对每个展览地点和时刻,计算能准时到达展览地点的汽车总数。
输入格式
第一行包含三个整数 $k, n, q$,表示「Lada Malina」的发动机数量、工厂数量、展览时间和地点的选项数,满足 $2 \leq k \leq 10$,$1 \leq n \leq 10^5$,$1 \leq q \leq 10^5$。
接下来的 $k$ 行,每行包含两个整数 $vx_{i}, vy_{i}$($-1000 \leq vx_{i}, vy_{i} \leq 1000$),为第 $i$ 台发动机的速度向量分量。任一发动机的速度向量不为零(即 $vx_{i}$、$vy_{i}$ 至少有一个不为零),且任意两台发动机的速度向量不共线(平行)。
接下来的 $n$ 行,每行包含三个整数 $fx_{i}, fy_{i}, a_{i}$,分别代表第 $i$ 个工厂的位置坐标及拥有的汽车数量($-10^9 \leq fx_{i}, fy_{i} \leq 10^9$,$1 \leq a_{i} \leq 10^9$)。
以下 $q$ 行,每行包含三个整数 $px_{i}, py_{i}, t_{i}$,表示第 $i$ 个展览选项的地点坐标及距离展览开始的天数($-10^9 \leq px_{i}, py_{i} \leq 10^9$,$1 \leq t_{i} \leq 10^5$)。
输出格式
对于每个展览选项,输出一个整数,表示能按时到达展览地点的汽车总数。
说明/提示
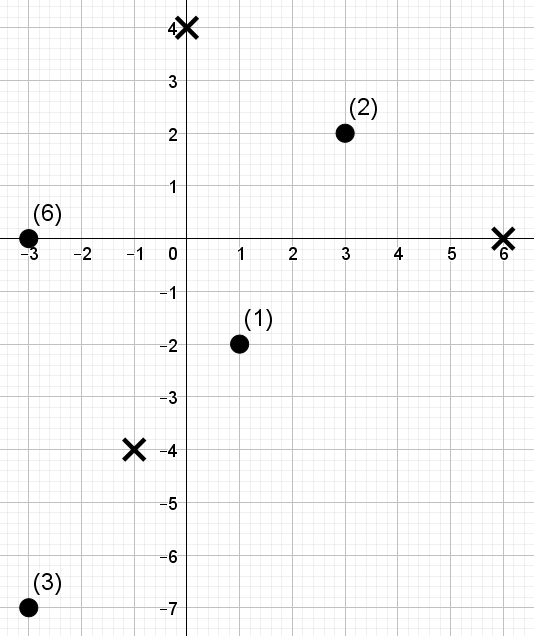
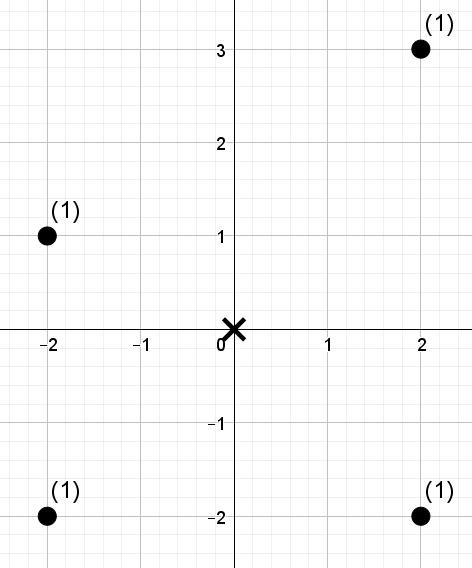
下图描述了样例测试。图中的叉号表示展览选项,圆点表示工厂位置。每个工厂旁标注了其车辆数。
样例一说明:
- 第一工厂无法准时赶到展览地点。
- 第二工厂的车辆可通过设置 $w_{1}=0$,$w_{2}=1$ 准时到达展览。
- 第三工厂的车辆可通过设置 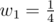,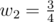 准时到达。
- 第四工厂的车辆可通过设置 $w_{1}=1$,$w_{2}=0$ 准时到达。
由 ChatGPT 5 翻译