CF863C 1-2-3

**题面** Ilya 从事机器人制作这一行业。Ilya 为娱乐机器人编程，目前他工作的项目是 "Bob"，新一代的游戏机器人。Ilya 的老板最近想知道他的进展如何，特别是如果 Bob 比以前的 Alice 更擅长玩不同的游戏，他会对此很感兴趣。 现在，Ilya 想知道他的机器人在一个简单的叫“ 1-2-3 ”的游戏中的表现。这个游戏类似于“石头、剪刀、布”的游戏：两个机器人同时 $3}$ 中选择一个数字，如果他们选择相同的数字，那么这是平局，没有人得分。但是，如果这两个数字不同，那么其中一个机器人能得一分。$3$ 能打败 $2$，而 $2$ 能打败 $1,1$ 能打败 $3$。 这两个机器人的程序使得他们在第 $(i+1)$ 局中的选择只依赖于第 $i$ 局的选择。 Ilya 知道机器人将会玩 $k$ 局游戏，Alice 机器人将会在第一局选择数字 $a$，而 Bob 机器人会选择数字 $b$。他也知道两个机器人的程序，可以根据他们在前一场比赛中的选择来判断每个机器人会选择什么。但 Ilya 太懒了不想等到机器人把那 $k$ 局游戏玩完，所以他请你来预测在最后一场比赛后每个机器人的得分。

第一行有三个整数 $k(1 \le k \le 10^{18}),a$ 和 $b(1 \le a,b \le 3)$。接下来三行，第 $i$ 行有 $A_{i,1}$ 以及 $A_{i,2}$ 和 $A_{i,3}$。$A_{i,j}$ 表示如果 Alice 选择了 $i$ 而 Bob 选择了 $j$ 时 Alice 的选择。下面又有 $3$ 行：第 $i$ 行有 $B_{i,1}$ 以及 $B_{i,2}$ 和 $B_{i,3}$。$B_{i,j}$ 表示如果 Alice 选择了 $i$ 而 Bob 选择了 $j$ 时 Bob 的选择。

两个整数，分别表示 Alice 的分数和 Bob 的分数。 感谢 @x義x 提供的翻译

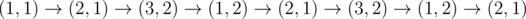
In the second example game goes like this:  The fourth and the seventh game are won by Bob, the first game is draw and the rest are won by Alice.