CF865C Gotta Go Fast
Description
You're trying to set the record on your favorite video game. The game consists of $ N $ levels, which must be completed sequentially in order to beat the game. You usually complete each level as fast as possible, but sometimes finish a level slower. Specifically, you will complete the $ i $ -th level in either $ F_{i} $ seconds or $ S_{i} $ seconds, where $ F_{i}<S_{i} $ , and there's a $ P_{i} $ percent chance of completing it in $ F_{i} $ seconds. After completing a level, you may decide to either continue the game and play the next level, or reset the game and start again from the first level. Both the decision and the action are instant.
Your goal is to complete all the levels sequentially in at most $ R $ total seconds. You want to minimize the expected amount of time playing before achieving that goal. If you continue and reset optimally, how much total time can you expect to spend playing?
Input Format
The first line of input contains integers $ N $ and $ R $ 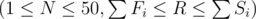, the number of levels and number of seconds you want to complete the game in, respectively. $ N $ lines follow. The $ i $ th such line contains integers $ F_{i},S_{i},P_{i} $ $ (1
Output Format
Print the total expected time. Your answer must be correct within an absolute or relative error of $ 10^{-9} $ .
Formally, let your answer be $ a $ , and the jury's answer be $ b $ . Your answer will be considered correct, if 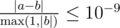.
Explanation/Hint
In the first example, you never need to reset. There's an $ 81% $ chance of completing the level in $ 2 $ seconds and a $ 19% $ chance of needing $ 8 $ seconds, both of which are within the goal time. The expected time is $ 0.81·2+0.19·8=3.14 $ .
In the second example, you should reset after the first level if you complete it slowly. On average it will take $ 0.25 $ slow attempts before your first fast attempt. Then it doesn't matter whether you complete the second level fast or slow. The expected time is $ 0.25·30+20+0.85·3+0.15·9=31.4 $ .