CF869C The Intriguing Obsession
题目描述
齐心协力,我们可以以超乎想象的速度到达任何地方!现在,火炎姐妹 (Fire Sisters) —— 火怜 (Karen) 和月火 (Tsukihi) 正在前往一个她们从未到达的地方——水中的小岛!
有三种不同类型的小岛,方便地,各自涂上了红,蓝,紫三色。每种颜色的小岛各自有 $a,b,c$ 个。
这些小岛之间初始时互相分离。可以在小岛之间架桥,两个小岛间最多架一座桥。
但要满足:任意两个不同的颜色相同的小岛的最短距离要大于等于 $3$(桥的长度为 $1$)。
火炎姐妹已经准备好迎接未知了,但是她们想测试一下你的勇气。你需要计算出不同的架桥方案有多少种,如果有两个小岛之间造桥的方案变了,我们就说这两个造桥的方案不同。答案对 $998244353$ 取模。
输入格式
一行三个正整数 $a,b,c$($1\le a,b,c\le 5000$),分别表示红、蓝、紫色小岛的个数。
输出格式
输出一个数,表示造桥的方案数,对 $998244353$ 取模。
Translated by @小粉兔
说明/提示
In the first example, there are $ 3 $ bridges that can possibly be built, and no setup of bridges violates the restrictions. Thus the answer is $ 2^{3}=8 $ .
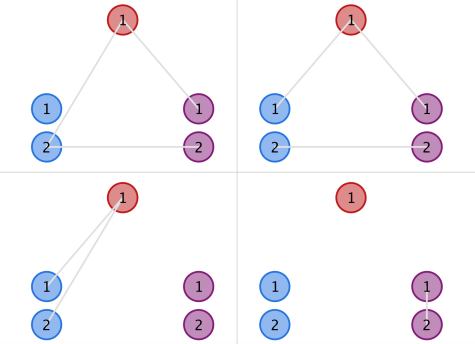
In the second example, the upper two structures in the figure below are instances of valid ones, while the lower two are invalid due to the blue and purple clusters, respectively.