CF870E Points, Lines and Ready-made Titles
题目描述
给定 $n$ 个位于平面上的不同点,每个点的坐标均为整数。对于每个点,你可以选择在该点上画一条竖直直线、画一条水平直线,或者什么都不做。
你认为所有重合的直线只算作一条。请问一共可以得到多少种不同的图案?答案对 $10^9+7$ 取模。
输入格式
第一行包含一个整数 $n$($1 \leq n \leq 10^5$),表示点的数量。
接下来 $n$ 行,每行包含两个整数 $x_i$ 和 $y_i$($-10^9 \leq x_i, y_i \leq 10^9$),表示第 $i$ 个点的坐标。
保证所有点互不相同。
输出格式
输出可以得到的不同图案数量,结果对 $10^9+7$ 取模。
说明/提示
在第一个样例中,通过这些点可以画出两条竖直直线和两条水平直线。你可以得到包含这些直线的任意子集的不同图案。例如,包含所有四条直线的图案可以从两种方式获得(图中的每一段表示一条经过该点的直线)。
第一种方式: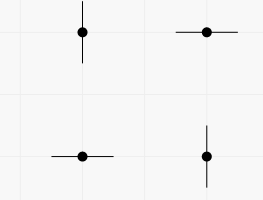
第二种方式: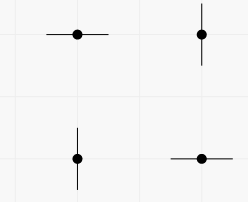
在第二个样例中,你可以独立地对每个点进行操作。图案的数量为 $3^2 = 9$。
由 ChatGPT 5 翻译