CF870F Paths
题目描述
给定一个正整数 $n$。我们在顶点 $1,2,\ldots,n$ 上构建一张图,当且仅当 $u$ 和 $v$ 满足下图条件时,在顶点 $u$ 和 $v$ 之间连一条边:
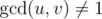
记 $d(u,v)$ 为顶点 $u$ 和 $v$ 之间的最短距离,如果不存在路径则 $d(u,v)=0$。请计算所有满足 $1 \leq u < v \leq n$ 的 $d(u,v)$ 之和。
两个正整数的 $gcd$(最大公约数)是能够同时整除这两个整数的最大正整数。
输入格式
输入一个整数 $n$,其中 $1 \leq n \leq 10^7$。
输出格式
输出所有满足 $1 \leq u < v \leq n$ 的 $d(u,v)$ 之和。
说明/提示
第一个样例中所有的最短路径如下:
- 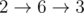
- 
- 
- 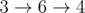
- 
- 
其他点对之间不存在路径。
总距离为 $2+1+1+2+1+1=8$。
由 ChatGPT 5 翻译