CF873A Chores

Luba has to do $ n $ chores today. $ i $ -th chore takes $ a_{i} $ units of time to complete. It is guaranteed that for every 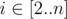 the condition $ a_{i}>=a_{i-1} $ is met, so the sequence is sorted. Also Luba can work really hard on some chores. She can choose not more than $ k $ any chores and do each of them in $ x $ units of time instead of $ a_{i} $ (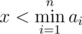). Luba is very responsible, so she has to do all $ n $ chores, and now she wants to know the minimum time she needs to do everything. Luba cannot do two chores simultaneously.

The first line contains three integers $ n,k,x (1

Print one number — minimum time Luba needs to do all $ n $ chores.

In the first example the best option would be to do the third and the fourth chore, spending $ x=2 $ time on each instead of $ a_{3} $ and $ a_{4} $ , respectively. Then the answer is $ 3+6+2+2=13 $ . In the second example Luba can choose any two chores to spend $ x $ time on them instead of $ a_{i} $ . So the answer is $ 100·3+2·1=302 $ .