CF891B Gluttony
题目描述
给定一个包含 $n$ 个互不相同整数的数组 $a$。请通过对 $a$ 进行排列构造出一个数组 $b$,使得对于任意非空且不包含全部元素的下标子集 $S = \{x_1, x_2, ..., x_k\}$(其中 $1 \le x_i \le n$,$0 < k < n$),在 $a$ 和 $b$ 的这些位置上的元素之和不同,即:
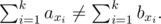
输入格式
第一行包含一个整数 $n$($1 \le n \le 22$),表示数组的大小。
第二行包含 $n$ 个用空格分隔的不同整数 $a_1, a_2, ..., a_n$($0 \le a_i \le 10^9$),表示数组 $a$ 的元素。
输出格式
如果不存在这样的数组 $b$,输出 -1。
否则,在一行中输出 $n$ 个用空格分隔的整数 $b_1, b_2, ..., b_n$。注意,$b$ 必须是 $a$ 的一个排列。
如果有多组答案,只需输出任意一组即可。
说明/提示
如果我们可以通过重新排列 $y$ 的元素,使其与 $x$ 完全一致,则称数组 $x$ 是 $y$ 的一个排列。
注意,空集和包含所有下标的子集不计入讨论范围。
由 ChatGPT 5 翻译