CF891C Envy

对于一个连通的无向带权图 $G$，MST（最小生成树）是 $G$ 的一个子图，包含 $G$ 的所有顶点，是一棵树，并且其所有边的权值之和尽可能小。 给定一个图 $G$。如果你在该图上运行最小生成树算法，只会得到一棵最小生成树，这就让其它边“嫉妒”了。你会得到若干个询问，每个询问包含 $G$ 的一个边集合，你需要判断是否存在一棵包含这些边的最小生成树。

第一行包含两个整数 $n,m$（$2 \leq n,m \leq 5 \cdot 10^5$，$n-1 \leq m$），表示图中顶点数和边数。 接下来 $m$ 行，每行三个整数 $u_i, v_i, w_i$（$u_i \neq v_i$，$1 \leq w_i \leq 5 \cdot 10^5$），表示第 $i$ 条边的两个端点和边权。两点之间可以有多条边。保证给定的图是连通的。 下一行包含一个整数 $q$（$1 \leq q \leq 5 \cdot 10^5$），表示询问数量。 接下来 $q$ 行，每行表示一次询问。第 $i$ 行以一个整数 $k_i$ 开头（$1 \leq k_i \leq n-1$），表示该边的子集大小，随后有 $k_i$ 个互不相同的、从 $1$ 到 $m$ 编号的边的编号。保证所有询问的 $k_i$ 之和不超过 $5 \cdot 10^5$。

对于每组询问，如果存在一个包含这些指定边的最小生成树，输出 "YES"；否则输出 "NO"。每个询问输出一行。

下面是样例的图示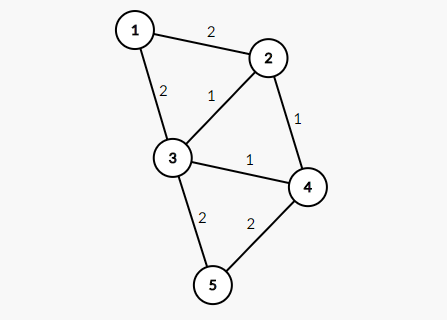：  该图的最小生成树权值为 $6$。 边集 $(1,3,4,6)$ 包含了第一个询问中的所有边，因此对第一个询问的答案是 "YES"。 第二个询问中的边构成了一个长为 $3$ 的环，因此没有最小生成树包含这三条边。所以答案为 "NO"。 由 ChatGPT 5 翻译