CF901B GCD of Polynomials
Description
Suppose you have two polynomials 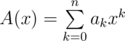 and 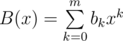. Then polynomial 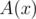 can be uniquely represented in the following way:
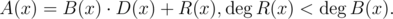This can be done using [long division](https://en.wikipedia.org/wiki/Polynomial_long_division). Here, 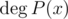 denotes the degree of polynomial $ P(x) $ . 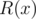 is called the remainder of division of polynomial 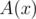 by polynomial 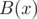, it is also denoted as 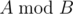.
Since there is a way to divide polynomials with remainder, we can define Euclid's algorithm of finding the greatest common divisor of two polynomials. The algorithm takes two polynomials 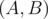. If the polynomial 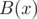 is zero, the result is 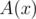, otherwise the result is the value the algorithm returns for pair 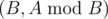. On each step the degree of the second argument decreases, so the algorithm works in finite number of steps. But how large that number could be? You are to answer this question.
You are given an integer $ n $ . You have to build two polynomials with degrees not greater than $ n $ , such that their coefficients are integers not exceeding $ 1 $ by their absolute value, the leading coefficients (ones with the greatest power of $ x $ ) are equal to one, and the described Euclid's algorithm performs exactly $ n $ steps finding their greatest common divisor. Moreover, the degree of the first polynomial should be greater than the degree of the second. By a step of the algorithm we mean the transition from pair 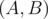 to pair 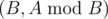.
Input Format
You are given a single integer $ n $ ( $ 1
Output Format
```plain
Print two polynomials in the following format.
```
In the first line print a single integer $ m $ ( $ 0
Explanation/Hint
In the second example you can print polynomials $ x^{2}-1 $ and $ x $ . The sequence of transitions is
$ (x^{2}-1,x)→(x,-1)→(-1,0). $ There are two steps in it.