CF901C Bipartite Segments
题目描述
给定一个无向图,该图有 $n$ 个顶点。图中不存在长度为偶数的边-简单环。换句话说,图中不存在长度为偶数且每条边最多经过一次的环。顶点编号为 $1$ 到 $n$。
你需要回答 $q$ 个询问。每个询问给出一个顶点区间 $[l;r]$,你需要统计该区间内有多少个子区间 $[x;y]$($l \leq x \leq y \leq r$),使得如果我们只保留顶点 $[x;y]$ 及其之间的边,删除其他顶点和相关边,则所得的图是二分图。
输入格式
第一行包含两个整数 $n$ 和 $m$($1 \leq n \leq 3\cdot 10^{5}$,$1 \leq m \leq 3\cdot 10^{5}$),分别表示图中的顶点数和边数。
接下来的 $m$ 行,每行描述一条边。第 $i$ 行包含两个整数 $a_{i}$ 和 $b_{i}$($1 \leq a_{i}, b_{i} \leq n$;$a_{i} \ne b_{i}$),表示顶点 $a_{i}$ 与 $b_{i}$ 间有一条边。保证该图中不存在长度为偶数的边-简单环。
接下来一行包含一个整数 $q$($1 \leq q \leq 3\cdot 10^{5}$),表示询问数。
接下来的 $q$ 行,每行两个整数 $l_{i}$ 和 $r_{i}$($1 \leq l_{i} \leq r_{i} \leq n$),表示一个询问的参数。
输出格式
输出 $q$ 行,每行一个数,第 $i$ 行输出仅包含顶点 $[l_{i}, r_{i}]$ 及其之间的边时构成二分图的子区间 $[x; y]$ 的数量。
说明/提示
第一个样例的图见下图:
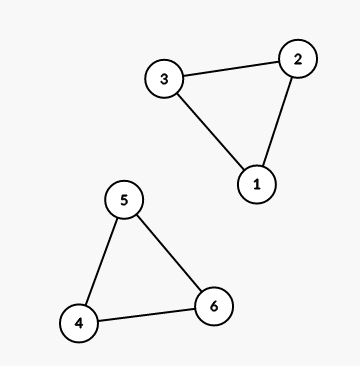
对于第一个询问,$[1;3]$ 除了整个区间本身外,其余子区间均符合条件。
对于第二个询问,$[4;6]$ 除了整个区间本身外,其余子区间均符合条件。
对于第三个询问,$[1;6]$ 的所有子区间,除了 $[1;3]$,$[1;4]$,$[1;5]$,$[1;6]$,$[2;6]$,$[3;6]$,$[4;6]$ 这些区间外,剩下的都符合条件。
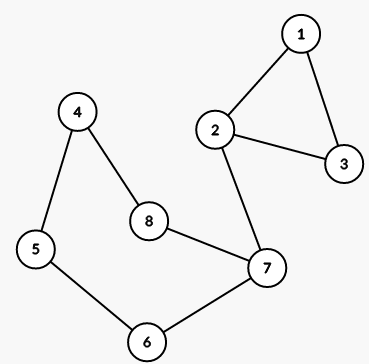
第二个样例见下图:
由 ChatGPT 5 翻译