CF901C Bipartite Segments

You are given an undirected graph with $ n $ vertices. There are no edge-simple cycles with the even length in it. In other words, there are no cycles of even length that pass each edge at most once. Let's enumerate vertices from $ 1 $ to $ n $ . You have to answer $ q $ queries. Each query is described by a segment of vertices $ [l;r] $ , and you have to count the number of its subsegments $ [x;y] $ ( $ l

The first line contains two integers $ n $ and $ m $ ( $ 1

Print $ q $ numbers, each in new line: the $ i $ -th of them should be the number of subsegments $ [x;y] $ ( $ l_{i}

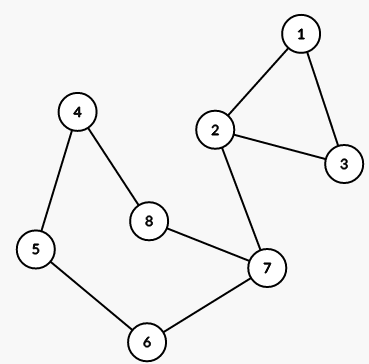
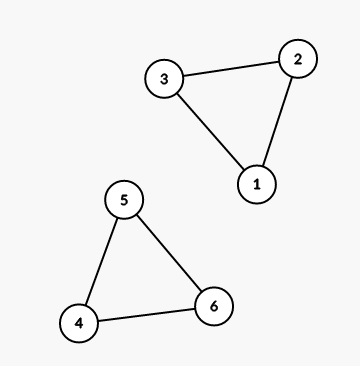
The first example is shown on the picture below:  For the first query, all subsegments of $ [1;3] $ , except this segment itself, are suitable. For the first query, all subsegments of $ [4;6] $ , except this segment itself, are suitable. For the third query, all subsegments of $ [1;6] $ are suitable, except $ [1;3] $ , $ [1;4] $ , $ [1;5] $ , $ [1;6] $ , $ [2;6] $ , $ [3;6] $ , $ [4;6] $ . The second example is shown on the picture below: