CF901C Bipartite Segments

给定一个无向图，该图有 $n$ 个顶点。图中不存在长度为偶数的边-简单环。换句话说，图中不存在长度为偶数且每条边最多经过一次的环。顶点编号为 $1$ 到 $n$。 你需要回答 $q$ 个询问。每个询问给出一个顶点区间 $[l;r]$，你需要统计该区间内有多少个子区间 $[x;y]$（$l \leq x \leq y \leq r$），使得如果我们只保留顶点 $[x;y]$ 及其之间的边，删除其他顶点和相关边，则所得的图是二分图。

第一行包含两个整数 $n$ 和 $m$（$1 \leq n \leq 3\cdot 10^{5}$，$1 \leq m \leq 3\cdot 10^{5}$），分别表示图中的顶点数和边数。 接下来的 $m$ 行，每行描述一条边。第 $i$ 行包含两个整数 $a_{i}$ 和 $b_{i}$（$1 \leq a_{i}, b_{i} \leq n$；$a_{i} \ne b_{i}$），表示顶点 $a_{i}$ 与 $b_{i}$ 间有一条边。保证该图中不存在长度为偶数的边-简单环。 接下来一行包含一个整数 $q$（$1 \leq q \leq 3\cdot 10^{5}$），表示询问数。 接下来的 $q$ 行，每行两个整数 $l_{i}$ 和 $r_{i}$（$1 \leq l_{i} \leq r_{i} \leq n$），表示一个询问的参数。

输出 $q$ 行，每行一个数，第 $i$ 行输出仅包含顶点 $[l_{i}, r_{i}]$ 及其之间的边时构成二分图的子区间 $[x; y]$ 的数量。

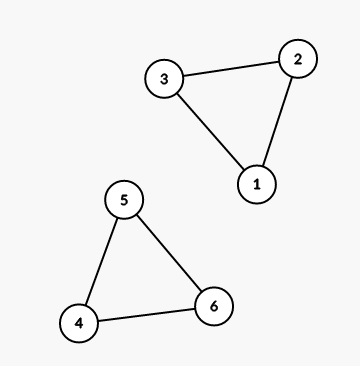
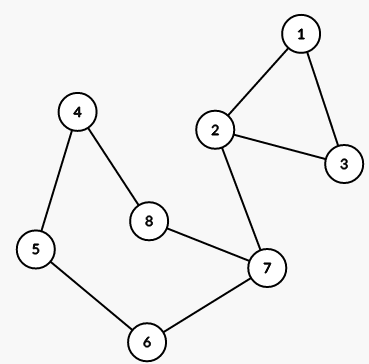
第一个样例的图见下图：  对于第一个询问，$[1;3]$ 除了整个区间本身外，其余子区间均符合条件。 对于第二个询问，$[4;6]$ 除了整个区间本身外，其余子区间均符合条件。 对于第三个询问，$[1;6]$ 的所有子区间，除了 $[1;3]$，$[1;4]$，$[1;5]$，$[1;6]$，$[2;6]$，$[3;6]$，$[4;6]$ 这些区间外，剩下的都符合条件。 第二个样例见下图：  由 ChatGPT 5 翻译