CF901E Cyclic Cipher

Senor Vorpal Kickass'o invented an innovative method to encrypt integer sequences of length $ n $ . To encrypt a sequence, one has to choose a secret sequence 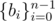, that acts as a key. Vorpal is very selective, so the key should be such a sequence $ b_{i} $ , that its cyclic shifts are linearly independent, that is, there is no non-zero set of coefficients $ x_{0},x_{1},...,x_{n-1} $ , such that 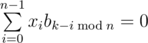 for all $ k $ at the same time. 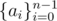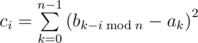After that for a sequence  you should build the following cipher: In other words, you are to compute the quadratic deviation between each cyclic shift of $ b_{i} $ and the sequence $ a_{i} $ . The resulting sequence is the Kickass's cipher. The cipher is in development right now and Vorpal wants to decipher a sequence after it has been encrypted. You are to solve this problem for him. You are given sequences $ c_{i} $ and $ b_{i} $ . You are to find all suitable sequences $ a_{i} $ .

The first line contains a single integer $ n $ (). The second line contains $ n $ integers $ b_{0},b_{1},...,b_{n-1} $ (). The third line contains $ n $ integers $ c_{0},c_{1},...,c_{n-1} $ (). It is guaranteed that all cyclic shifts of sequence $ b_{i} $ are linearly independent.

In the first line print a single integer $ k $ — the number of sequences $ a_{i} $ , such that after encrypting them with key $ b_{i} $ you get the sequence $ c_{i} $ . After that in each of $ k $ next lines print $ n $ integers $ a_{0},a_{1},...,a_{n-1} $ . Print the sequences in lexicographical order. Note that $ k $ could be equal to $ 0 $ .