CF902B Coloring a Tree
题目描述
给定一棵有 $n$ 个结点的有根树。结点编号为 $1$ 到 $n$,根结点编号为 $1$。
每个结点有一个颜色,设第 $v$ 个结点的颜色为 $c_v$。初始时 $c_v=0$。
你需要用尽可能少的步数将树染成指定的颜色。每一步你可以选择一个结点 $v$ 和一种颜色 $x$,然后将 $v$ 的子树(包括 $v$ 本身)中的所有结点染成颜色 $x$。也就是说,对于每个从根到 $u$ 的路径经过 $v$ 的结点 $u$,都将其颜色 $c_u$ 设为 $x$。
保证需要将每个结点染成不为 $0$ 的颜色。
你可以通过查看该链接了解有根树:https://en.wikipedia.org/wiki/Tree\_(graph\_theory)。
输入格式
第一行包含一个整数 $n$($2 \le n \le 10^{4}$)——树的结点数。
第二行包含 $n-1$ 个整数 $p_2, p_3, ..., p_n$($1 \le p_i < i$),其中 $p_i$ 表示存在一条连接结点 $i$ 和 $p_i$ 的边。
第三行包含 $n$ 个整数 $c_1, c_2, ..., c_n$($1 \le c_i \le n$),其中 $c_i$ 表示你最终要将第 $i$ 个结点染成的颜色。
保证给定的图是一棵树。
输出格式
输出一个整数——将树染成指定颜色所需的最少操作次数。
说明/提示
第一个样例对应的树见下图(数字为结点编号):
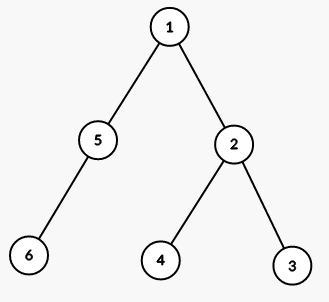
第一步,将以结点 $1$ 为根的子树的所有结点染成颜色 $2$(图上数字为颜色):
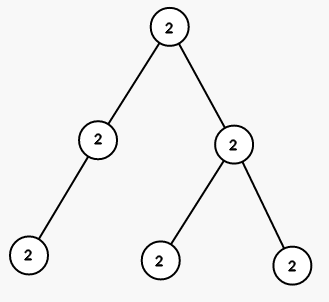
第二步,将以结点 $5$ 为根的子树的所有结点染成颜色 $1$:
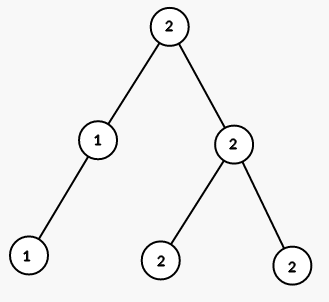
第三步,将以结点 $2$ 为根的子树的所有结点染成颜色 $1$:
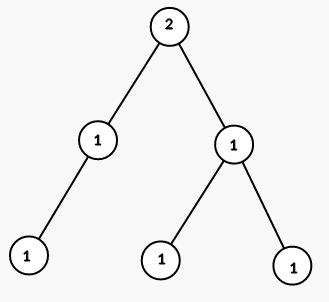
第二个样例对应的树见下图(数字为结点编号):
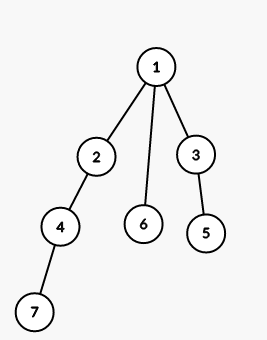
第一步,将以结点 $1$ 为根的子树的所有结点染成颜色 $3$:
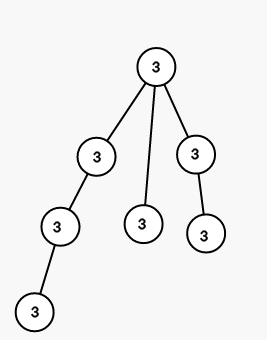
第二步,将以结点 $3$ 为根的子树的所有结点染成颜色 $1$:
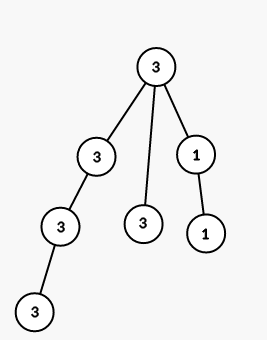
第三步,将以结点 $6$ 为根的子树的所有结点染成颜色 $2$:
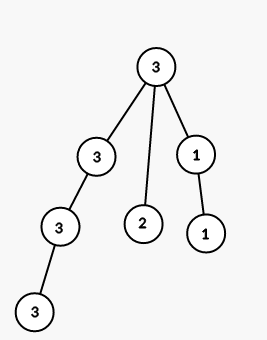
第四步,将以结点 $4$ 为根的子树的所有结点染成颜色 $1$:
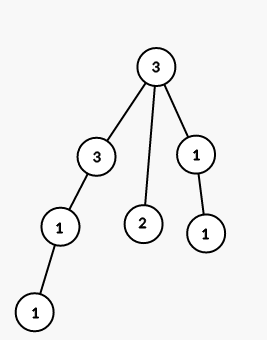
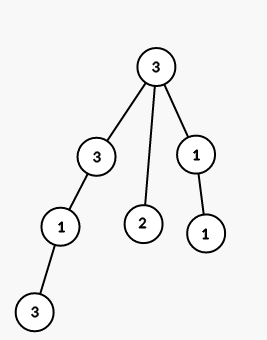
第五步,将以结点 $7$ 为根的子树的所有结点染成颜色 $3$:
由 ChatGPT 5 翻译