CF902B Coloring a Tree

You are given a rooted tree with $ n $ vertices. The vertices are numbered from $ 1 $ to $ n $ , the root is the vertex number $ 1 $ . Each vertex has a color, let's denote the color of vertex $ v $ by $ c_{v} $ . Initially $ c_{v}=0 $ . You have to color the tree into the given colors using the smallest possible number of steps. On each step you can choose a vertex $ v $ and a color $ x $ , and then color all vectices in the subtree of $ v $ (including $ v $ itself) in color $ x $ . In other words, for every vertex $ u $ , such that the path from root to $ u $ passes through $ v $ , set $ c_{u}=x $ . It is guaranteed that you have to color each vertex in a color different from $ 0 $ . You can learn what a rooted tree is using the link: https://en.wikipedia.org/wiki/Tree\_(graph\_theory).

The first line contains a single integer $ n $ ( $ 2

Print a single integer — the minimum number of steps you have to perform to color the tree into given colors.

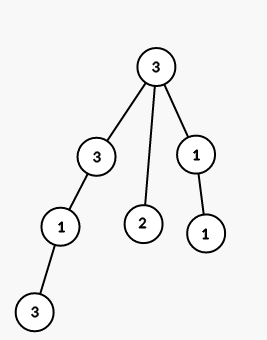
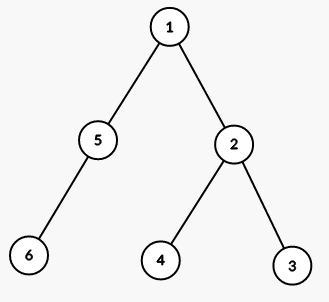
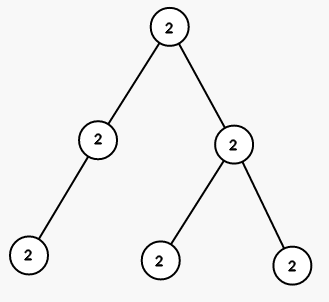
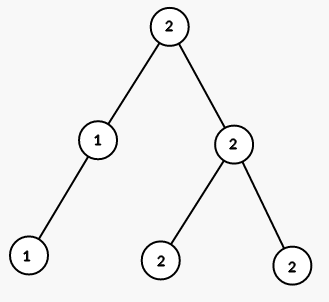
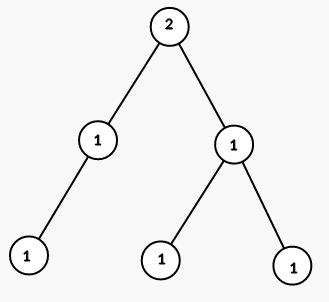
The tree from the first sample is shown on the picture (numbers are vetices' indices):  On first step we color all vertices in the subtree of vertex $ 1 $ into color $ 2 $ (numbers are colors):  On seond step we color all vertices in the subtree of vertex $ 5 $ into color $ 1 $ :  On third step we color all vertices in the subtree of vertex $ 2 $ into color $ 1 $ :  The tree from the second sample is shown on the picture (numbers are vetices' indices):  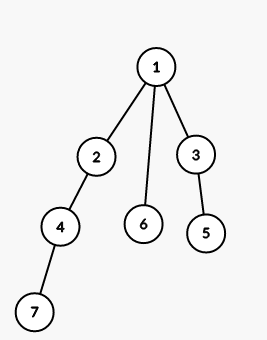On first step we color all vertices in the subtree of vertex $ 1 $ into color $ 3 $ (numbers are colors):  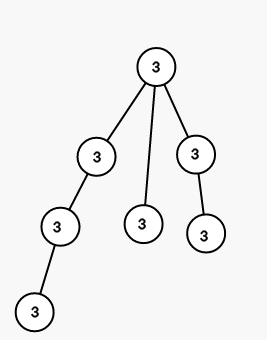On second step we color all vertices in the subtree of vertex $ 3 $ into color $ 1 $ :  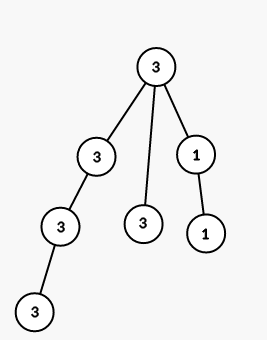On third step we color all vertices in the subtree of vertex $ 6 $ into color $ 2 $ :  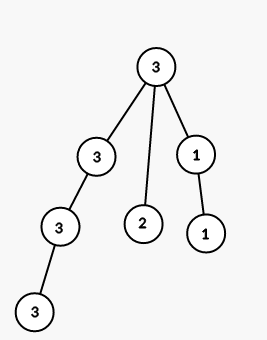On fourth step we color all vertices in the subtree of vertex $ 4 $ into color $ 1 $ :  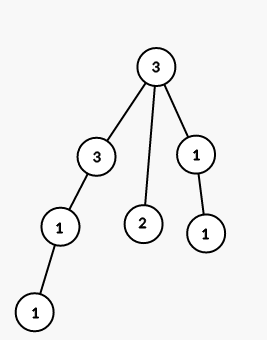On fith step we color all vertices in the subtree of vertex $ 7 $ into color $ 3 $ :