CF903D Almost Difference
题目描述
我们定义函数
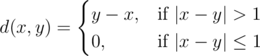
现在给定一个由 $n$ 个整数组成的数组 $a$。请你计算所有满足 $1 \leq i \leq j \leq n$ 的 $(i, j)$ 对应的 $d(a_i, a_j)$ 之和。
输入格式
第一行包含一个整数 $n$($1 \leq n \leq 200000$),表示数组 $a$ 的元素个数。
第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$($1 \leq a_i \leq 10^9$),表示数组的各个元素。
输出格式
输出一个整数,表示所有满足 $1 \leq i \leq j \leq n$ 的 $(i, j)$ 对应的 $d(a_i, a_j)$ 之和。
说明/提示
在第一个样例中:
1. $d(a_1, a_2)=0$;
2. $d(a_1, a_3)=2$;
3. $d(a_1, a_4)=0$;
4. $d(a_1, a_5)=2$;
5. $d(a_2, a_3)=0$;
6. $d(a_2, a_4)=0$;
7. $d(a_2, a_5)=0$;
8. $d(a_3, a_4)=-2$;
9. $d(a_3, a_5)=0$;
10. $d(a_4, a_5)=2$。
由 ChatGPT 5 翻译