CF903G Yet Another Maxflow Problem

在本题中，你需要处理一个非常特殊的网络。 该网络由两部分组成：部分 $A$ 和部分 $B$。每一部分均包含 $n$ 个顶点；第 $i$ 个部分 $A$ 的顶点记作 $A_{i}$，第 $i$ 个部分 $B$ 的顶点记作 $B_{i}$。 对于每个下标 $i$（$1 \leq i < n$），都存在一条有向边从顶点 $A_{i}$ 指向 $A_{i+1}$，以及一条有向边从 $B_{i}$ 指向 $B_{i+1}$。这些边的容量将在输入中给出。此外，部分 $A$ 到部分 $B$ 之间还可能存在若干有向边（但绝不会有从 $B$ 到 $A$ 的边）。 你需要计算该网络中从 $A_{1}$ 到 $B_{n}$ 的最大流值（maximum flow value）。部分 $A$ 内的 $A_{i}$ 到 $A_{i+1}$ 的边的容量有时会发生改变，你还需要维护每次改变之后的最大流值。除此之外，网络的其它部分（包括 $B$ 部分的边和 $A$ 到 $B$ 的边）都是固定的，不会发生变化，也不会有边的插入或删除。 请参考例子和提示更好地理解本题网络的结构。

第一行包含三个整数 $n$、$m$ 和 $q$（$2 \leq n, m \leq 2 \cdot 10^{5}$，$0 \leq q \leq 2 \cdot 10^{5}$），分别表示每部分的顶点数、$A$ 到 $B$ 的边数以及操作次数。 接下来 $n-1$ 行，每行包含两个整数 $x_{i}$ 和 $y_{i}$，分别表示 $A_{i}$ 到 $A_{i+1}$ 的边的容量为 $x_{i}$，$B_{i}$ 到 $B_{i+1}$ 的边的容量为 $y_{i}$（$1 \leq x_{i}, y_{i} \leq 10^{9}$）。 然后接下来 $m$ 行，描述 $A$ 到 $B$ 的边。每行包含三个整数 $x$、$y$ 和 $z$，表示从 $A_{x}$ 到 $B_{y}$ 的一条容量为 $z$ 的边（$1 \leq x, y \leq n$，$1 \leq z \leq 10^{9}$）。同一个点对之间可能有多重边。 最后 $q$ 行，每行包含两个整数 $v_{i}$ 和 $w_{i}$，表示将 $A_{v_{i}}$ 到 $A_{v_{i} + 1}$ 的边容量设置为 $w_{i}$（$1 \leq v_{i} < n$，$1 \leq w_{i} \leq 10^{9}$）。

首先输出初始网络的最大流值。接下来输出 $q$ 个整数，第 $i$ 个数表示第 $i$ 次操作后的最大流值。

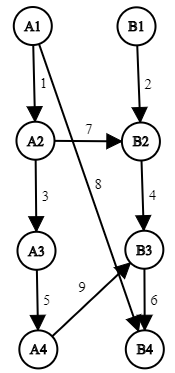
下面是示例中原始网络的结构：  由 ChatGPT 5 翻译