CF906D Power Tower
题目描述
羽蛇神教的祭司们希望建造一座高塔,以代表他们神的力量。高塔通常由蕴含能量的岩石组成。祭司们通过罕见的魔法将塔顶悬浮起来,并在底部加入新的岩石。如果当前由 $k-1$ 块岩石组成的塔顶拥有能量 $p$,我们现在要在底部加入一块能量为 $w_{k}$ 的岩石,则新高塔的能量为 $w_{k}^{p}$。
岩石的加入顺序是从后往前的。即对于序列 $w_1, ..., w_m$,能量值为
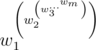高塔建成后,它的能量值可能非常巨大。但祭司们依然希望获得一些信息,他们想知道一个被称作“累积能量”的数值,即实际能量对 $m$ 取模后的结果。祭司们有 $n$ 块岩石,编号从 $1$ 到 $n$。他们请你计算,如果用编号从 $l$ 到 $r$ 的岩石来搭建高塔,高塔的累积能量是多少。
输入格式
第一行输入两个整数 $n$($1 \leq n \leq 10^5$)和 $m$($1 \leq m \leq 10^9$)。
第二行输入 $n$ 个整数 $w_k$($1 \leq w_k \leq 10^9$),表示祭司们拥有的每块岩石的能量。
第三行输入一个整数 $q$($1 \leq q \leq 10^5$),表示祭司的询问数。
接下来的 $q$ 行,每行输入两个整数 $l_k$ 和 $r_k$($1 \leq l_k \leq r_k \leq n$),表示用编号从 $l_k$ 到 $r_k$ 的岩石来建塔。
输出格式
输出 $q$ 行,每行一个整数,第 $k$ 行表示用编号 $l_k, l_k+1, ..., r_k$ 的岩石搭建的高塔最终累积能量。
说明/提示
$3^{27} = 7625597484987$。
由 ChatGPT 5 翻译