CF908C New Year and Curling

Carol is currently curling. She has $ n $ disks each with radius $ r $ on the 2D plane. Initially she has all these disks above the line $ y=10^{100} $ . She then will slide the disks towards the line $ y=0 $ one by one in order from $ 1 $ to $ n $ . When she slides the $ i $ -th disk, she will place its center at the point $ (x_{i},10^{100}) $ . She will then push it so the disk’s $ y $ coordinate continuously decreases, and $ x $ coordinate stays constant. The disk stops once it touches the line $ y=0 $ or it touches any previous disk. Note that once a disk stops moving, it will not move again, even if hit by another disk. Compute the $ y $ -coordinates of centers of all the disks after all disks have been pushed.

The first line will contain two integers $ n $ and $ r $ ( $ 1

Print a single line with $ n $ numbers. The $ i $ -th number denotes the $ y $ -coordinate of the center of the $ i $ -th disk. The output will be accepted if it has absolute or relative error at most $ 10^{-6} $ . Namely, let's assume that your answer for a particular value of a coordinate is $ a $ and the answer of the jury is $ b $ . The checker program will consider your answer correct if 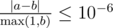 for all coordinates.

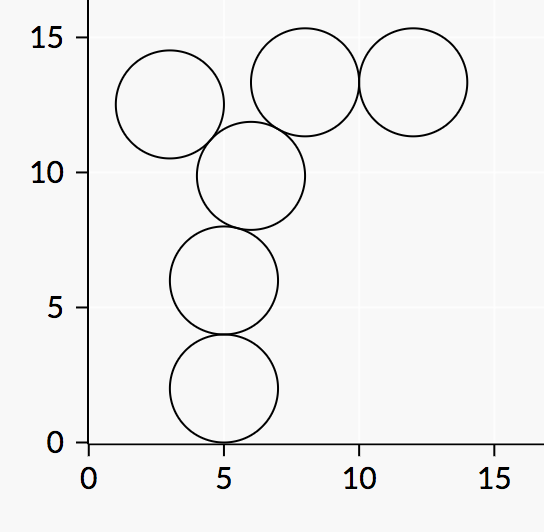The final positions of the disks will look as follows: In particular, note the position of the last disk.