CF908C New Year and Curling
题目描述
Carol 目前正在进行冰壶游戏。
她在二维平面上有 $n$ 个半径为 $r$ 的圆盘。
一开始,这些圆盘的中心都在直线 $y=10^{100}$ 之上。
接下来,她会按顺序从 $1$ 到 $n$,依次将每个圆盘滑向 $y=0$ 这条直线。
当她滑动第 $i$ 个圆盘时,会把它的圆心放在点 $(x_{i}, 10^{100})$。接着,她会推动圆盘,使其 $y$ 坐标不断减小,而 $x$ 坐标保持不变。圆盘会一直向下滑,直到遇到 $y=0$ 这条直线,或者碰到前面已经停止的任何一个圆盘为止。需要注意的是,一旦圆盘停止后,不会再被其他圆盘推动或移动。
请你计算,所有圆盘在推动完毕后的圆心 $y$ 坐标。
输入格式
第一行包含两个整数 $n$ 和 $r$($1 \leq n, r \leq 1000$),分别表示圆盘的数量以及圆盘的半径。
第二行包含 $n$ 个整数 $x_1, x_2, ..., x_n$($1 \leq x_i \leq 1000$),依次表示每个圆盘的 $x$ 坐标。
输出格式
输出一行共 $n$ 个数字,第 $i$ 个数字表示第 $i$ 个圆盘的圆心 $y$ 坐标。在满足绝对误差或相对误差不超过 $10^{-6}$ 的情况下,均为正确答案。
即,假设你输出的某个 $y$ 坐标为 $a$,标程输出为 $b$,如果对于所有坐标都有
$$
\frac{|a-b|}{\max(1, |b|)} \leq 10^{-6}
$$
则你的答案将被判为正确。
说明/提示
圆盘最终的位置如下图所示:
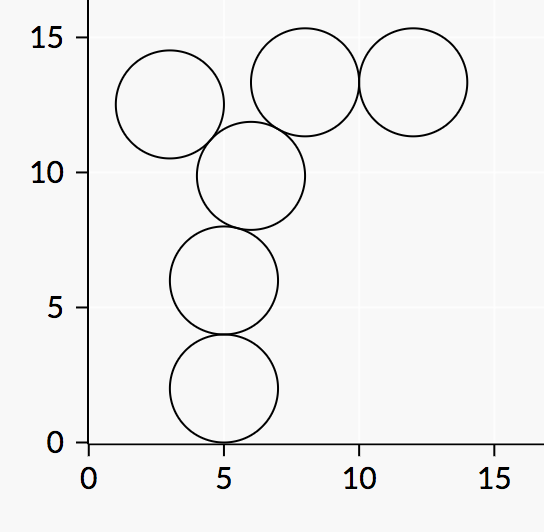
特别注意最后一个圆盘的位置。
由 ChatGPT 5 翻译