CF908E New Year and Entity Enumeration

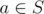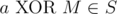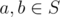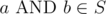
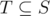
You are given an integer $ m $ . Let $ M=2^{m}-1 $ . You are also given a set of $ n $ integers denoted as the set $ T $ . The integers will be provided in base 2 as $ n $ binary strings of length $ m $ . A set of integers $ S $ is called "good" if the following hold. 1. If , then . 2. If , then  3.  4. All elements of $ S $ are less than or equal to $ M $ . Here, 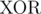 and 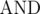 refer to the bitwise XOR and bitwise AND operators, respectively. Count the number of good sets $ S $ , modulo $ 10^{9}+7 $ .

The first line will contain two integers $ m $ and $ n $ ( $ 1

Print a single integer, the number of good sets modulo $ 10^{9}+7 $ .

An example of a valid set $ S $ is {00000, 00101, 00010, 00111, 11000, 11010, 11101, 11111}.