CF908H New Year and Boolean Bridges
题目描述
你的朋友有一个有 $n$ 个点的隐藏有向图。
定义 $f(u,v)$ 表示是否存在从节点 $u$ 到节点 $v$ 的有向路径,若存在则为真,否则为假。对于每对不同的节点 $u, v$,你知道如下三个陈述中至少有一个为真:
1. 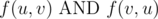
2. 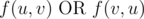
3. 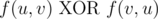
其中 AND、OR 和 XOR 分别表示与、或、异或运算。
你会得到一个 $n \times n$ 的矩阵,表示每对顶点哪一个陈述成立。矩阵的第 $u$ 行第 $v$ 列包含一个字符,具有以下含义:
1. 如果第一个陈述成立,用字符 ‘A’ 表示。
2. 如果第二个陈述成立,用字符 ‘O’ 表示。
3. 如果第三个陈述成立,用字符 ‘X’ 表示。
4. 对角线上仅包含字符 ‘-’。
注意,同一对节点可能同时满足多个条件,但给定的字符只代表其中某一个成立。该矩阵保证是对称的。
你想知道是否存在一个与这个矩阵一致的有向图。如果不存在,输出 -1。否则,输出最少需要多少条边可以与这些信息相符。
输入格式
第一行包含一个整数 $n$($1 \leq n \leq 47$),表示节点数量。
接下来 $n$ 行每行包含 $n$ 个字符,表示如题述的连接性矩阵。
输出格式
输出与所给信息相符的最小边数,如果不存在可行解,输出 $-1$。
说明/提示
样例 1:隐藏图是一个强连通图。你可以将所有四个节点首尾相连成一个环。
样例 2:一种可行的图是 $3 \to 1 \to 2$。对于每一对不同的节点,恰有一个 $f(u,v)$ 或 $f(v,u)$ 为真。
由 ChatGPT 5 翻译