CF913A Modular Exponentiation
Description
The following problem is well-known: given integers $ n $ and $ m $ , calculate
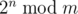, where $ 2^{n}=2·2·...·2 $ ( $ n $ factors), and 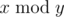 denotes the remainder of division of $ x $ by $ y $ .
You are asked to solve the "reverse" problem. Given integers $ n $ and $ m $ , calculate
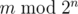.
Input Format
The first line contains a single integer $ n $ ( $ 1
Output Format
Output a single integer — the value of 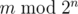.
Explanation/Hint
In the first example, the remainder of division of 42 by $ 2^{4}=16 $ is equal to 10.
In the second example, 58 is divisible by $ 2^{1}=2 $ without remainder, and the answer is 0.