CF915G Coprime Arrays

Let's call an array $ a $ of size $ n $ coprime iff $ gcd(a_{1},a_{2},...,a_{n})=1 $ , where $ gcd $ is the greatest common divisor of the arguments. You are given two numbers $ n $ and $ k $ . For each $ i $ ( $ 1

The first line contains two integers $ n $ and $ k $ ( $ 1

Since printing $ 2·10^{6} $ numbers may take a lot of time, you have to output the answer in such a way: Let $ b_{i} $ be the number of coprime arrays with elements in range $ [1,i] $ , taken modulo $ 10^{9}+7 $ . You have to print 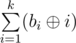, taken modulo $ 10^{9}+7 $ . Here  denotes bitwise xor operation (^ in C++ or Java, xor in Pascal).

Explanation of the example: Since the number of coprime arrays is large, we will list the arrays that are non-coprime, but contain only elements in range $ [1,i] $ : For $ i=1 $ , the only array is coprime. $ b_{1}=1 $ . For $ i=2 $ , array $ [2,2,2] $ is not coprime. $ b_{2}=7 $ . For $ i=3 $ , arrays $ [2,2,2] $ and $ [3,3,3] $ are not coprime. $ b_{3}=25 $ . For $ i=4 $ , arrays $ [2,2,2] $ , $ [3,3,3] $ , $ [2,2,4] $ , $ [2,4,2] $ , $ [2,4,4] $ , $ [4,2,2] $ , $ [4,2,4] $ , $ [4,4,2] $ and $ [4,4,4] $ are not coprime. $ b_{4}=55 $ .