CF916B Jamie and Binary Sequence (changed after round)
题目描述
Jamie 正在准备一次 Codeforces 比赛。他有了一个题目的想法,但不知道如何解决。请帮助他完成如下问题:
找到 $k$ 个整数,使得每个整数的 $2$ 的幂的和等于数字 $n$,且答案中的最大整数尽可能小。如果有多组答案,请输出字典序最大的那一组。
更明确地说,考虑所有长度为 $k$ 的整数序列 $(a_{1},a_{2},...,a_{k})$,满足 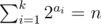。给每个序列赋予 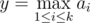 的取值。在所有 $y$ 值最小的序列中,输出字典序最大的那一个。
幂和字典序的定义见提示。
输入格式
第一行包含两个整数 $n$ 和 $k$($1\leq n\leq 10^{18}, 1\leq k\leq 10^{5}$)——需要得到的和与序列的长度。
输出格式
如果不存在这样的序列,输出一行“No”(不带引号)。否则,第一行输出“Yes”,第二行输出用空格隔开的 $k$ 个整数,表示所求序列。
保证答案序列中的整数均在区间 $[-10^{18},10^{18}]$ 范围内。
说明/提示
样例 1:
$2^{3}+2^{3}+2^{2}+2^{1}+2^{0}=8+8+4+2+1=23$
像 $(3,3,2,0,1)$ 或 $(0,1,2,3,3)$ 这样的答案不是字典序最大。
像 $(4,1,1,1,0)$ 这样的答案不具有最小的 $y$ 值。
样例 2:
可以证明不存在长度为 $2$ 的序列。
样例 3:
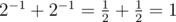
$2$ 的幂:
如果 $x>0$,那么 $2^x=2 \cdot 2 \cdot 2 \cdots 2$($x$ 个 $2$ 相乘)。
如果 $x=0$,那么 $2^x=1$。
如果 $x